题目内容
8.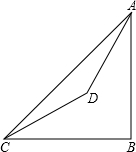 如图,在山脚C测得山顶A的仰角为45°,沿着倾斜角为30°的斜坡前进300米到达D出,D处测得山顶的仰角为60°,求山高AB(结果保留根号).
如图,在山脚C测得山顶A的仰角为45°,沿着倾斜角为30°的斜坡前进300米到达D出,D处测得山顶的仰角为60°,求山高AB(结果保留根号).
分析 首先根据题意分析图形;作DE⊥AB于E,作DF⊥BC于F,构造两个直角三角形,分别求解可得DF与EA的值,再利用图形关系,进而可求出答案.
解答  解:作DE⊥AB于E,作DF⊥BC于F,在Rt△CDF中∠DCF=30°,CD=300米,
解:作DE⊥AB于E,作DF⊥BC于F,在Rt△CDF中∠DCF=30°,CD=300米,
∴DF=CD•sin30°=$\frac{1}{2}$×300=150(米)
CF=CD•cos30°=$\frac{\sqrt{3}}{2}$×300=$\frac{300\sqrt{3}}{2}$(米)
在Rt△ADE中,∠ADE=60°,设DE=x米,
∴AE=tan60°•x=$\sqrt{3}$x(米)
在矩形DEBF中,BE=DF=150米,
在Rt△ACB中,∠ACB=45°,
∴AB=BC,
即:$\sqrt{3}$x+150=$\frac{300\sqrt{3}}{2}$+x
∴x=150,
∴AB=AE+BE=($\frac{300\sqrt{3}}{2}$+150)米.
点评 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知扇形的圆心角为60°,半径为5,则扇形的周长为( )
| A. | $\frac{5}{3}$π | B. | $\frac{5}{3}$π+10 | C. | $\frac{5}{6}$ | D. | $\frac{5}{6}$π+10 |
 如图,在△ABC中,BC边上有n个点(包括B、C两点),则图中共有多少个三角形?
如图,在△ABC中,BC边上有n个点(包括B、C两点),则图中共有多少个三角形?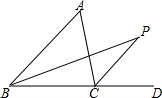 已知在△ABC中,内角∠ABC的平分线与外角∠ACD的平分线交于点P,试说明:∠P=$\frac{1}{2}$∠A.
已知在△ABC中,内角∠ABC的平分线与外角∠ACD的平分线交于点P,试说明:∠P=$\frac{1}{2}$∠A.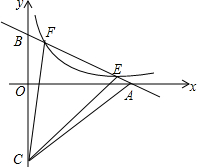 如图,直线y=-$\frac{1}{2}$x+b(b>0)与双曲线y=$\frac{1}{x}$(x>0)交于E、F两点,与x轴、y轴分别交于A、B两点,点C(0,-$\frac{3}{2}$b),连接CA,CB,CE,CF,若S△CEF=2(S△CAE+S△CBF),求b的值.
如图,直线y=-$\frac{1}{2}$x+b(b>0)与双曲线y=$\frac{1}{x}$(x>0)交于E、F两点,与x轴、y轴分别交于A、B两点,点C(0,-$\frac{3}{2}$b),连接CA,CB,CE,CF,若S△CEF=2(S△CAE+S△CBF),求b的值.