题目内容
3. 如图,一段河坝的横截面为梯形ABCD,根据图中数据,可知底宽AD=7.5+4$\sqrt{3}$(单位:m).
如图,一段河坝的横截面为梯形ABCD,根据图中数据,可知底宽AD=7.5+4$\sqrt{3}$(单位:m).
分析 作BF⊥AD于点于F,在直角△ABF中利用勾股定理即可求得AF的长,在直角△CED中,利用坡比的定义即可求得ED的长度,进而求得AD的长.
解答 解:作BF⊥AD于点F.则BF=CE=4m,EF=BC=4.5m.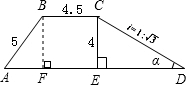
在Rt△ABF中,AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3m,
在Rt△CED中,根据i=$\frac{CE}{ED}$,
则ED=$\frac{CE}{i}$=$\frac{4}{\frac{1}{\sqrt{3}}}$=4$\sqrt{3}$m.
则AD=AF+EF+ED=3+4.5+4$\sqrt{3}$=(7.5+4$\sqrt{3}$)m.
答:坝底宽AD为(7.5+4$\sqrt{3}$)m.
点评 本题考查了坡度坡角的问题,把梯形的计算通过作高线转化成直角三角形的计算是解决本题的基本思路.

练习册系列答案
相关题目
13.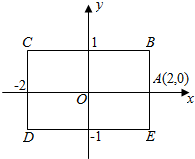 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )| A. | (-1,1) | B. | (-2,0) | C. | (-1,-1) | D. | (1,-1) |
8.-2,0,1,3这几个数中绝对值最小的数是( )
| A. | -2 | B. | 0 | C. | 1 | D. | 3 |
15.若(x-2)(x+3)=x2+ax+b,则a、b的值分别为( )
| A. | a=5,b=6 | B. | a=1,b=-6 | C. | a=1,b=6 | D. | a=5,b=-6 |
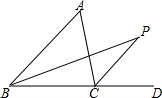 已知在△ABC中,内角∠ABC的平分线与外角∠ACD的平分线交于点P,试说明:∠P=$\frac{1}{2}$∠A.
已知在△ABC中,内角∠ABC的平分线与外角∠ACD的平分线交于点P,试说明:∠P=$\frac{1}{2}$∠A.