题目内容
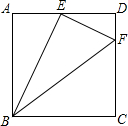如图，在□ABCD中，E是AD的中点，F是CD上一点，且CF=3FD．图中有几对相似三角形？把它们表示出来，并说明理由．考点：相似三角形的判定,正方形的性质
专题：常规题型
分析：设正方形的边长为4a，则AE=DE=2a，DF=a，CF=3a，理由勾股定理计算出BF=5a，BE=2
a，EF=
a，理由勾股定理的逆定理可证明△BEF为直角三角形，∠BEF=90°，再计算
=
=2，
=
=2，则
=
，根据相似三角形的判定即可得到Rt△ABE∽Rt△DEF，同理得Rt△ABE∽Rt△EBF，Rt△EBF∽Rt△DEF．
| 5 |
| 5 |
| AE |
| DF |
| 2a |
| a |
| AB |
| DE |
| 4a |
| 2a |
| AE |
| DF |
| AB |
| DE |
解答：解：有三对相似三角形，Rt△ABE∽Rt△DEF，Rt△ABE∽Rt△EBF，Rt△EBF∽Rt△DEF．理由如下：
设正方形的边长为4a，则AE=DE=2a，DF=a，CF=3a，
在Rt△BCF中，BF=
=5a，
在Rt△ABE中，BE=
=2
a，
在Rt△DEF中，EF=
=
a，
∵BE2+EF2=BF2，
∴△BEF为直角三角形，∠BEF=90°，
∵
=
=2，
=
=2，
∴
=
，
∴Rt△ABE∽Rt△DEF，
同理得
=
，
∴Rt△ABE∽Rt△EBF，
∴Rt△EBF∽Rt△DEF．
设正方形的边长为4a，则AE=DE=2a，DF=a，CF=3a，
在Rt△BCF中，BF=
| BC2+CF2 |
在Rt△ABE中，BE=
| AB2+AE2 |
| 5 |
在Rt△DEF中，EF=
| DF2+DE2 |
| 5 |
∵BE2+EF2=BF2，
∴△BEF为直角三角形，∠BEF=90°，
∵
| AE |
| DF |
| 2a |
| a |
| AB |
| DE |
| 4a |
| 2a |
∴
| AE |
| DF |
| AB |
| DE |
∴Rt△ABE∽Rt△DEF，
同理得
| AB |
| BE |
| AE |
| EF |
∴Rt△ABE∽Rt△EBF，
∴Rt△EBF∽Rt△DEF．
点评：本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．也考查了勾股定理的逆定理．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
如图，点A，B，C，D，E，F分别在⊙O上，AC=BD，CE=DF，连接AE，BF．△ACE与△BDF全等吗？为什么？
在Rt△ABC中，∠ACB=90°，D在AB中点，AE⊥CD于点M，
如图所示，E，F分别为平行四边形的边AD，BC中点，且?ABFF∽?ADCB，则AB：BC等于如图，从边长为（a+4）的正方形纸片中剪去一个边长为（a+1）的正方形（a＞0），剩余部分沿虚线又剪拼成一个长方形（不重叠、无缝隙），若拼成的长方形一边的长为3，则另一边的长为（ ）
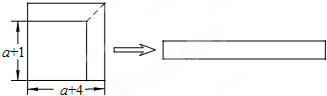
| A、2a+5 | B、2a+8 |
| C、2a+3 | D、2a+2 |