题目内容
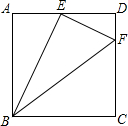
如图所示，E，F分别为平行四边形的边AD，BC中点，且?ABFF∽?ADCB，则AB：BC等于考点：相似多边形的性质
专题：
分析：首先利用E，F分别为平行四边形的边AD，BC中点，得到AE=BF=
AD=
BC，然后根据?ABFF∽?ADCB，得到
=
，从而整理得到
=
，求得结论．
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| AB |
| AB |
| BC |
| AB2 |
| BC2 |
| 1 |
| 2 |
解答：解：∵E，F分别为平行四边形的边AD，BC中点，
∴AE=BF=
AD=
BC，
∵?ABFF∽?ADCB，
∴
=
即：AB2=AE•BC=
BC•BC=
BC2，
∴
=
，
∴
=
，
故答案为：
：2．
∴AE=BF=
| 1 |
| 2 |
| 1 |
| 2 |
∵?ABFF∽?ADCB，
∴
| AE |
| AB |
| AB |
| BC |
即：AB2=AE•BC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AB2 |
| BC2 |
| 1 |
| 2 |
∴
| AB |
| BC |
| ||
| 2 |
故答案为：
| 2 |
点评：本题考查了相似多边形的性质，解题的关键是了解相似多边形的对应边的比相等，对应角相等．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
如图，在□ABCD中，E是AD的中点，F是CD上一点，且CF=3FD．图中有几对相似三角形？把它们表示出来，并说明理由．
如图，在⊙O中，弦AB，CD相交于点P，且AB=CD，求证：AC=BD．某商品的进价是400元，标价为600元，折价销售时的利润为5%，问此商品是按几折销售的？设此商品按x%销售，由题意得方程为（ ）
| A、600•x%=400×5% |
| B、400（1+5%）=6000•x% |
| C、400（1-5%）+600•x% |
| D、600（1-5%）=400•x% |