题目内容
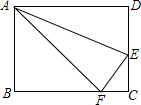 在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离.
在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离.考点:矩形的性质,勾股定理
专题:
分析:求出BF,然后判断出△ABF和△BCF都是等腰直角三角形,再根据等腰直角三角形的性质可得∠AFB=∠CFE=45°,然后求出∠AFE=90°,再利用勾股定理列式求出AF、EF、AE,然后利用三角形的面积公式列方程求解即可.
解答:解:∵BC=8,CF=2,
∴BF=8-2=6,
∴△ABF和△BCF都是等腰直角三角形,
∴∠AFB=∠CFE=45°,
∴∠AFE=90°,
由勾股定理得,AF=
AB=6
,
EF=
CE=2
,
AE=
=
=4
,
设点F到AE的距离为h,
则S△AEF=
AE•h=
AE•EF,
即
×4
•h=
×6
×2
,
解得h=
,
即点F到AE的距离是
.
∴BF=8-2=6,
∴△ABF和△BCF都是等腰直角三角形,
∴∠AFB=∠CFE=45°,
∴∠AFE=90°,
由勾股定理得,AF=
| 2 |
| 2 |
EF=
| 2 |
| 2 |
AE=
| AD2+DE2 |
| 82+(6-2)2 |
| 5 |
设点F到AE的距离为h,
则S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 2 |
| 2 |
解得h=
6
| ||
| 5 |
即点F到AE的距离是
6
| ||
| 5 |
点评:本题考查了矩形的性质,勾股定理,等腰直角三角形的判定与性质,三角形的面积,解题的关键在于判断出∠AFE=90°.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 如图,△ABC是⊙O的内接三角形,AB=AC,D是BC上一点,AD的延长线交⊙O于点E.
如图,△ABC是⊙O的内接三角形,AB=AC,D是BC上一点,AD的延长线交⊙O于点E. 如图,已知
如图,已知 如图所示,求半径为2的圆内接正方形的边心距与面积.
如图所示,求半径为2的圆内接正方形的边心距与面积. 如图:AC是⊙O的直径,弦CB平分∠ECA,BE⊥EC交⊙o于点D,连接AB、AD、BD.
如图:AC是⊙O的直径,弦CB平分∠ECA,BE⊥EC交⊙o于点D,连接AB、AD、BD.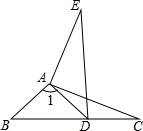 如图,若△ABC≌△ADE,且∠B=38°,则∠1=
如图,若△ABC≌△ADE,且∠B=38°,则∠1= 如图,直线与x轴相交于点A,与y轴相交于点B.
如图,直线与x轴相交于点A,与y轴相交于点B.