题目内容
 如图,△ABC是⊙O的内接三角形,AB=AC,D是BC上一点,AD的延长线交⊙O于点E.
如图,△ABC是⊙O的内接三角形,AB=AC,D是BC上一点,AD的延长线交⊙O于点E.(1)△ABE与△CDE相似吗?为什么?
(2)图中还有哪几对相似三角形?
考点:相似三角形的判定,圆周角定理
专题:
分析:(1)根据等边对等角可得∠ABC=∠ACB,再根据等弧所对的圆周角相等可得∠AEB=∠AEC,∠BAE=∠ECD,然后根据两组角对应相等的三角形相似证明;
(2)确定出相等的角,再根据两组角对应相等的三角形相似解答.
(2)确定出相等的角,再根据两组角对应相等的三角形相似解答.
解答:(1)解:∵AB=AC,
∴∠ABC=∠ACB,
∴∠AEB=∠AEC,∠BAE=∠ECD,
∴△ABE∽△CDE;
(2)解:∠AEB=ACB=∠ABC=∠AEC,
∠EBC=∠EAC,
相似三角形有:△ABD∽△AEB,△ABD∽△CED,△ACD∽△BED.
∴∠ABC=∠ACB,
∴∠AEB=∠AEC,∠BAE=∠ECD,
∴△ABE∽△CDE;
(2)解:∠AEB=ACB=∠ABC=∠AEC,
∠EBC=∠EAC,
相似三角形有:△ABD∽△AEB,△ABD∽△CED,△ACD∽△BED.
点评:本题考查了相似三角形的判定,圆周角定理,熟记定理并确定出相等的角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是一些大小相同的小正方体组成的几何体,则其俯视图是( )
如图是一些大小相同的小正方体组成的几何体,则其俯视图是( )A、 |
B、 |
C、 |
D、 |
某校对初三(2)班40名学生体育考试中“立定跳远”项目的得分情况进行了统计,结果如表所示:
根据表中数据,可以知道这次“立定跳远”成绩的中位数是 .
| 得分 | 10分 | 9分 | 8分 | 7分 | 6分以下 |
| 人数(人) | 20 | 12 | 5 | 2 | 1 |
地球的半径是6370km,用科学记数法表示是( )米.
| A、6.37×103 |
| B、637×101 |
| C、63.7×105 |
| D、6.37×106 |
 如图,已知∠AOB:∠BOC:∠COD=2:1:3,且∠AOC+∠DOB=150°,求∠AOD的度数.
如图,已知∠AOB:∠BOC:∠COD=2:1:3,且∠AOC+∠DOB=150°,求∠AOD的度数.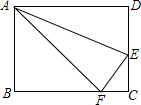 在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离.
在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离.