题目内容
 如图,直线与x轴相交于点A,与y轴相交于点B.
如图,直线与x轴相交于点A,与y轴相交于点B.(1)已知OA=2,AB=2
| 5 |
(2)直线AB上有点P,若△BOP的面积为8,试求P点的坐标.
考点:待定系数法求一次函数解析式,一次函数图象上点的坐标特征
专题:计算题
分析:(1)在直角三角形AOB中,由AB与OA的长,利用勾股定理求出OB的长,确定出B坐标,设直线解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可确定出解析式;
(2)分两种情况考虑:当A为BP中点时,可得三角形BOP面积等于2倍三角形AOB面积,即为8,求出P坐标;当BP=2AB时,可得三角形BOP面积等于2倍三角形AOB面积,即为8,求出P坐标,综上,得到满足题意P的坐标.
(2)分两种情况考虑:当A为BP中点时,可得三角形BOP面积等于2倍三角形AOB面积,即为8,求出P坐标;当BP=2AB时,可得三角形BOP面积等于2倍三角形AOB面积,即为8,求出P坐标,综上,得到满足题意P的坐标.
解答: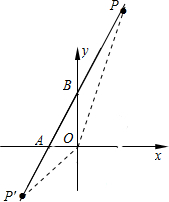 解:(1)∵OA=2,AB=2
解:(1)∵OA=2,AB=2
,
∴根据勾股定理得:OB=
=4,
A(-2,0),B(0,4),
设直线AB解析式为y=kx+b,
把A与B坐标代入得:
,
解得:k=2,b=4,
则直线解析式为y=2x+4;
(2)∵OA=2,OB=4,
∴△AOB面积为
×2×4=4,
∵△BOP面积为8,
∴分两种情况考虑:当A为BP中点时,△BOP面积=2△AOB面积=8,
此时P坐标为(-4,-4);
当BP=2AB时,△BOP面积=2△AOB面积=8,
设P坐标为(x,2x+4),
则有BP=2AB=4
,即
=4
,
解得:x=4,
此时P(4,12),
综上,满足题意的P坐标为(-4,-4),(4,12).
 解:(1)∵OA=2,AB=2
解:(1)∵OA=2,AB=2| 5 |
∴根据勾股定理得:OB=
| AB2-OA2 |
A(-2,0),B(0,4),
设直线AB解析式为y=kx+b,
把A与B坐标代入得:
|
解得:k=2,b=4,
则直线解析式为y=2x+4;
(2)∵OA=2,OB=4,
∴△AOB面积为
| 1 |
| 2 |
∵△BOP面积为8,
∴分两种情况考虑:当A为BP中点时,△BOP面积=2△AOB面积=8,
此时P坐标为(-4,-4);
当BP=2AB时,△BOP面积=2△AOB面积=8,
设P坐标为(x,2x+4),
则有BP=2AB=4
| 5 |
| x2+(2x+4-4)2 |
| 5 |
解得:x=4,
此时P(4,12),
综上,满足题意的P坐标为(-4,-4),(4,12).
点评:此题考查了待定系数法求一次函数解析式,以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
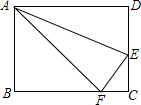 在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离.
在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离.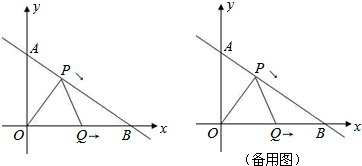
 如图,从一个大正方形中截去面积为12cm2和18cm2的两个小正方形,你能求出原来大正方形的面积吗?
如图,从一个大正方形中截去面积为12cm2和18cm2的两个小正方形,你能求出原来大正方形的面积吗?