题目内容
在平面直角坐标系中我们把横坐标和纵坐标相等的点成称为梦之点.例如点(-1,-1),(0,0),(
,
),…都是“梦之点”,显然这样的“梦之点”有无数个.
(1)若点P(2,m)是正比例函数y=nx的图象上的“梦之点”,求这个正比例函数的解析式;
(2)函数y=3x-5的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)函数y=kx-k+1(k≠1)的图象上有“梦之点”吗?若存在,请求出“梦之点”的坐标,若不存在,请说明理由.
| 2 |
| 2 |
(1)若点P(2,m)是正比例函数y=nx的图象上的“梦之点”,求这个正比例函数的解析式;
(2)函数y=3x-5的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)函数y=kx-k+1(k≠1)的图象上有“梦之点”吗?若存在,请求出“梦之点”的坐标,若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据梦之点的定义,可得P点坐标,根据待定系数法,可得函数解析式;
(2)根据梦之点的横坐标与纵坐标相同,可得关于a的方程,根据解方程,可得答案;
(3)根据梦之点的横坐标与纵坐标相同,可得关于b的方程,根据解方程,可得答案.
(2)根据梦之点的横坐标与纵坐标相同,可得关于a的方程,根据解方程,可得答案;
(3)根据梦之点的横坐标与纵坐标相同,可得关于b的方程,根据解方程,可得答案.
解答:解:(1)由点P(2,m)是正比例函数y=nx的图象上的“梦之点”,得
m=2,即P(2,2).
把P(2,2)代入y=nx,得n=1,
这个正比例函数的解析式y=x;
(2)函数y=3x-5的图象上存在“梦之点”,设“梦之点”是(a,a),
把(a,a)代入y=3x-5得
a=3a-5.
解得a=
,即“梦之点”是(
,
),
故函数y=3x-5的图象上的“梦之点”是(
,
);
(3)函数y=kx-k+1(k≠1)的图象上有“梦之点”,设“梦之点”是(b,b),
把(b,b)代入y=kx-k+1(k≠1),得b=kb-k+1.
化简,得b-kb=1-k.
解得b=1,
即“梦之点”是(1,1),
故函数y=kx-k+1(k≠1)的图象上有“梦之点”是(1,1).
m=2,即P(2,2).
把P(2,2)代入y=nx,得n=1,
这个正比例函数的解析式y=x;
(2)函数y=3x-5的图象上存在“梦之点”,设“梦之点”是(a,a),
把(a,a)代入y=3x-5得
a=3a-5.
解得a=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
故函数y=3x-5的图象上的“梦之点”是(
| 5 |
| 2 |
| 5 |
| 2 |
(3)函数y=kx-k+1(k≠1)的图象上有“梦之点”,设“梦之点”是(b,b),
把(b,b)代入y=kx-k+1(k≠1),得b=kb-k+1.
化简,得b-kb=1-k.
解得b=1,
即“梦之点”是(1,1),
故函数y=kx-k+1(k≠1)的图象上有“梦之点”是(1,1).
点评:本题考查了一次函数的综合题,利用了“梦之点”的定义,解一元一次方程.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,则sinA的值为( )
如图,在Rt△ABC中,∠C=90°,则sinA的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
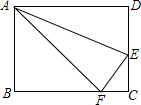 在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离.
在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离. 如图,从一个大正方形中截去面积为12cm2和18cm2的两个小正方形,你能求出原来大正方形的面积吗?
如图,从一个大正方形中截去面积为12cm2和18cm2的两个小正方形,你能求出原来大正方形的面积吗?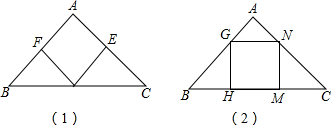
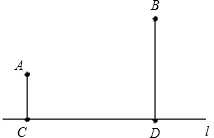 如图,A、B是一条河l同侧的两个村庄,且A、B两个村庄到河的距离分别是3千米和5千米,两村庄之间的距离AB为2
如图,A、B是一条河l同侧的两个村庄,且A、B两个村庄到河的距离分别是3千米和5千米,两村庄之间的距离AB为2