题目内容
 如图:AC是⊙O的直径,弦CB平分∠ECA,BE⊥EC交⊙o于点D,连接AB、AD、BD.
如图:AC是⊙O的直径,弦CB平分∠ECA,BE⊥EC交⊙o于点D,连接AB、AD、BD.(1)猜想BE与⊙O的位置关系,并证明你的猜想;
(2)求证:BD=BA;
(3)若AB=12,BC=5,求CD的长.
考点:切线的判定
专题:
分析:(1)如图,作辅助线;证明△BCE≌△BCF,得到∠EBC=∠FBC,∠OBC=∠OCB;根据∠OCB+∠FBC=90°,即可解决问题.
(2)证明∠BAD=∠BDA,即可解决问题.
(3)首先求出AC,进而求出FC;求出BF;根据勾股定理求出DE,即可解决问题.
(2)证明∠BAD=∠BDA,即可解决问题.
(3)首先求出AC,进而求出FC;求出BF;根据勾股定理求出DE,即可解决问题.
解答: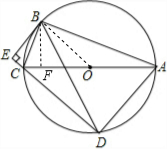 解:(1)猜想:BE与⊙O相切;证明如下:
解:(1)猜想:BE与⊙O相切;证明如下:
如图,连接OB;过点B作BF⊥OC于点F;
∵BE⊥EC,弦CB平分∠ECA,
∴BE=BF;
在直角△BCE与直角△BFC中,
,
∴△BCE≌△BCF(HL),
∠EBC=∠FBC;
∵OB=OC,
∴∠OBC=∠OCB;
∵BF⊥AC,
∴∠OCB+∠FBC=90°,故∠OBC+∠EBC=90°,
∴BE与⊙O相切.
(2)∵ ∠BAD=∠BCE,∠BCA=∠BDA,而∠BCE=∠BCF,
∠BAD=∠BCE,∠BCA=∠BDA,而∠BCE=∠BCF,
∴∠BAD=∠BDA,
∴BD=BA.
(3)∵AC为⊙O的直径,
∴∠ABC=90°;
由勾股定理得:AC2=AB2+BC2,而AB=12,BC=5,
∴AC=13;由射影定理得:BC2=CF•AC,
∴CF=
;由勾股定理得:BF2=BC2-CF2,
∴BF=
;由△BCE≌△BCF得:
BE=BF=
,CE=CF=
,BD=AB=12;
由勾股定理得:DE2=BD2-BE2,
∴DE=
,CD=
-
=
;
即CD的长为
.
 解:(1)猜想:BE与⊙O相切;证明如下:
解:(1)猜想:BE与⊙O相切;证明如下:如图,连接OB;过点B作BF⊥OC于点F;
∵BE⊥EC,弦CB平分∠ECA,
∴BE=BF;
在直角△BCE与直角△BFC中,
|
∴△BCE≌△BCF(HL),
∠EBC=∠FBC;
∵OB=OC,
∴∠OBC=∠OCB;
∵BF⊥AC,
∴∠OCB+∠FBC=90°,故∠OBC+∠EBC=90°,
∴BE与⊙O相切.
(2)∵
 ∠BAD=∠BCE,∠BCA=∠BDA,而∠BCE=∠BCF,
∠BAD=∠BCE,∠BCA=∠BDA,而∠BCE=∠BCF,∴∠BAD=∠BDA,
∴BD=BA.
(3)∵AC为⊙O的直径,
∴∠ABC=90°;
由勾股定理得:AC2=AB2+BC2,而AB=12,BC=5,
∴AC=13;由射影定理得:BC2=CF•AC,
∴CF=
| 25 |
| 13 |
∴BF=
| 60 |
| 13 |
BE=BF=
| 60 |
| 13 |
| 25 |
| 13 |
由勾股定理得:DE2=BD2-BE2,
∴DE=
| 144 |
| 13 |
| 144 |
| 13 |
| 25 |
| 13 |
| 119 |
| 13 |
即CD的长为
| 119 |
| 13 |
点评:该题主要考查了切线的判定、勾股定理、射影定理及其应用问题;解题的关键是深入观察分析、大胆猜测推理、科学求解论证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
地球的半径是6370km,用科学记数法表示是( )米.
| A、6.37×103 |
| B、637×101 |
| C、63.7×105 |
| D、6.37×106 |
 已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.
已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.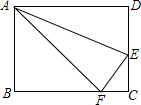 在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离.
在矩形ABCD,AB=6,BC=8,点E、F分别在DC、BC上,且CE=CF=2,求点F到AE的距离.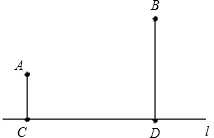 如图,A、B是一条河l同侧的两个村庄,且A、B两个村庄到河的距离分别是3千米和5千米,两村庄之间的距离AB为2
如图,A、B是一条河l同侧的两个村庄,且A、B两个村庄到河的距离分别是3千米和5千米,两村庄之间的距离AB为2