题目内容
10.在一条数轴上有A、B两点,点A表示数-4,点B表示数6,点P是该数轴上的一个动点(不与A、B重合)表示数x.点M、N分别是线段AP、BP的中点(1)如果点P在线段AB上,则点M表示的数是$\frac{-4+x}{2}$,则点N表示的数是$\frac{x+6}{2}$(用含x的代数式表示),并计算线段MN的长;
(2)如果点P在点B右侧,请你计算线段MN的长;
(3)如果点P在点A左侧,则线段MN的长度会改变吗?如果改变,请说明理由;如果不变,请直接写出结果.
分析 (1)、(2)、(3)根据题意画出图形,用x表示出MN表示的数,再由数轴上两点间的距离公式即可得出结论.
解答 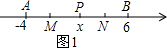 解:(1)如图1所示,
解:(1)如图1所示,
∵点A表示数-4,点B表示数6,点P表示数x,点M、N分别是线段AP、BP的中点,
∴点M表示$\frac{-4+x}{2}$,点N表示$\frac{x+6}{2}$,
∴MN=$\frac{x+6}{2}$-$\frac{-4+x}{2}$=5,
故答案为:$\frac{-4+x}{2}$,$\frac{x+6}{2}$;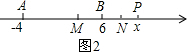
(2)如图2所示,
∵点A表示数-4,点B表示数6,点P表示数x,点M、N分别是线段AP、BP的中点,
∴点M表示$\frac{-4+x}{2}$,点N表示$\frac{x+6}{2}$,
∴MN=$\frac{x+6}{2}$-$\frac{-4+x}{2}$-=5;
(3)不会改变,MN=5,理由同(2).
点评 本题考查的是数轴,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
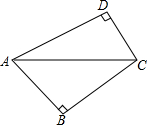 如图,四边形ABCD的一组对角∠ABC、∠ADC都是直角.
如图,四边形ABCD的一组对角∠ABC、∠ADC都是直角. 已知:△ABC中,ED∥BC,BD与CE交于点O,连接AO并延长交BC于点M,求证:M是BC中点.
已知:△ABC中,ED∥BC,BD与CE交于点O,连接AO并延长交BC于点M,求证:M是BC中点.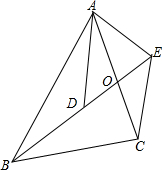 如图,四边形ABCE中,AC与BE交于点O,D是BO上一点,已知AD=4,△ABD∽△ACE.
如图,四边形ABCE中,AC与BE交于点O,D是BO上一点,已知AD=4,△ABD∽△ACE. 已知E为△ABC的AC边的中点,过E作FD,交AB于D,交BC的延长线于F.求证:AD•BF=BD•CF.
已知E为△ABC的AC边的中点,过E作FD,交AB于D,交BC的延长线于F.求证:AD•BF=BD•CF.