题目内容
20.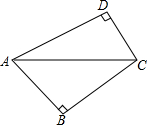 如图,四边形ABCD的一组对角∠ABC、∠ADC都是直角.
如图,四边形ABCD的一组对角∠ABC、∠ADC都是直角.求证:A、B、C、D四点在同一个圆上.
分析 取AC的中点O,连接OD、OB,根据直角三角形的性质得到OD=$\frac{1}{2}$AC,OB=$\frac{1}{2}$AC,得到OA=OB=OC=OD,得到答案.
解答 证明: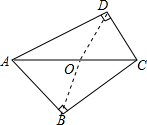 取AC的中点O,连接OD、OB,
取AC的中点O,连接OD、OB,
∵∠ABC是直角,O为AC的中点,
∴OD=$\frac{1}{2}$AC,
∵∠ADC都是直角,O为AC的中点,
∴OB=$\frac{1}{2}$AC,
∴OA=OB=OC=OD,
∴A、B、C、D四点在以O为圆心、以$\frac{1}{2}$AC为半径的同一个圆上.
点评 本题考查的是直角三角形的性质和圆的认识,掌握直角三角形斜边上的中线等于斜边的一半、到定点的距离等于定长的点在同一个圆上是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
8.化简x<2|1-$\sqrt{2}$|+1的结果是( )
| A. | x<2-$\sqrt{2}$ | B. | x<2$\sqrt{2}$-1 | C. | x<2 | D. | x<$\sqrt{2}$ |
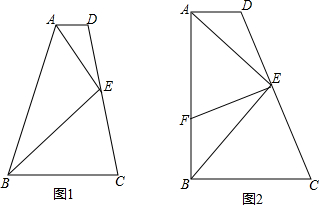
 如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=$\sqrt{3}$,求当顶点A运动到A″位置时,点A经过的路径长度.
如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=$\sqrt{3}$,求当顶点A运动到A″位置时,点A经过的路径长度.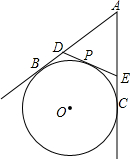 已知:如图,AB,AC是⊙O的切线,B,C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB,AC分别交于点D,E.
已知:如图,AB,AC是⊙O的切线,B,C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB,AC分别交于点D,E.