题目内容
4.定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为$\frac{n}{{2}^{k}}$(其中k是使$\frac{n}{{2}^{k}}$为奇数的正整数),并且运算重复进行.例如,取n=18时,则: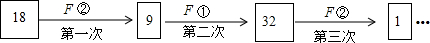
若n=31,则第31次“F运算”的结果是1.
分析 根据运算规则进行重复计算,从中发现循环的规律,得到答案.
解答 解:根据题意得,
当n=18时,第1次的计算结果是$\frac{18}{2}$=9;
第2次的计算结果是9×3+5=32;
第3次的计算结果是$\frac{32}{{2}^{5}}$=1;
第4次是计算结果是1×3+5=8;
第5次的计算结果是$\frac{8}{{2}^{3}}$=1,开始循环;
…31-18=15,15÷4=3…3,
故第31次的计算结果是1,
故答案为:1.
点评 此题主要考查了数字的变化规律,理解运算法则,利用运算法则运算,发现规律是解答本题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
16.已知2a=3,2b=6,2c=12,则a,b,c之间满足的关系是( )
| A. | a+b=c | B. | ab=c | C. | 2b=a+c | D. | 无法确定 |
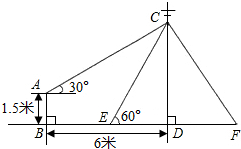 如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
 如图,AD∥BC,BE平分∠ABC,∠BED=145°,则∠BAD=110°.
如图,AD∥BC,BE平分∠ABC,∠BED=145°,则∠BAD=110°.
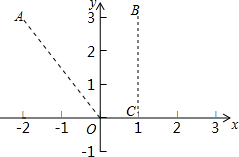 对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小的长度为G1、G2的“密距”.如图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k的值为-4.
对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小的长度为G1、G2的“密距”.如图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k的值为-4.