题目内容
13.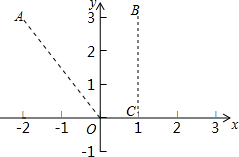 对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小的长度为G1、G2的“密距”.如图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k的值为-4.
对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小的长度为G1、G2的“密距”.如图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k的值为-4.
分析 由题意设双曲线上的D到直线的距离最近,过D作直线l和直线y=x-1的平行线,结合条件可求得l的解析式,联立l与双曲线解析式,则该方程组只有一组解,可求得k的值.
解答 解:
根据“密距”的定义可知双曲线图象在二、四象限,且离第四象限最近,
设双曲线上点D到直线y=x-1距离最近,如图,设直线y=x-1与y轴交于点E,过D作直线y=x-1的平行线,交y轴于点G,过D作直线y=x-1的垂线,垂足为E,过E作EH⊥DG,垂足为H,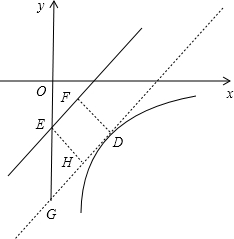
则由题意可知DF=EH=$\frac{3\sqrt{2}}{2}$,
又∠OEF=45°,
∴∠EGH=45°,
∴EH=HG=$\frac{3\sqrt{2}}{2}$,
∴EG=$\sqrt{2}$EH=$\sqrt{2}$×$\frac{3\sqrt{2}}{2}$=3,
又OE=1,
∴OG=4,
∴直线DG的解析式为y=x-4,
根据对称性可知点D坐标为(2,-2),
∴k=-4
故答案为:-4.
点评 本题考查了反比例函数与一次函数的交点问题,根据所给定义结合图形求得与双曲线只有一个交点的直线解析式是解题的关键.

练习册系列答案
相关题目
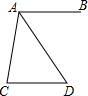 如图,AB∥CD,AD平分∠BAC,且∠C=80°,求∠D的度数.
如图,AB∥CD,AD平分∠BAC,且∠C=80°,求∠D的度数.
 如图,两个正方形边长分别是10厘米和6厘米,求阴影部分的面积.
如图,两个正方形边长分别是10厘米和6厘米,求阴影部分的面积.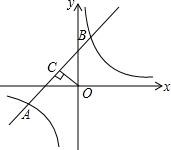 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+2的图象的一个交点为A(m,-1).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+2的图象的一个交点为A(m,-1).