题目内容
19.将抛物线y=x2-4x+3向上平移至顶点落在x轴上,如图所示,将两条抛物线、对称轴和y轴围成的图形的面积S(图中的阴影部分)是2.
分析 把点A、B、C代入抛物线解析式y=ax2+bx+c利用待定系数法求解即可;把抛物线解析式整理成顶点式形式,然后写出顶点坐标;根据顶点坐标求出向上平移的距离,再根据阴影部分的面积等于平行四边形的面积,列式进行计算即可得解.
解答  解:∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),
解:∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),
∴$\left\{\begin{array}{l}{c=3}\\{9a+3b+c=0}\\{16a+4b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$,
∴抛物线的函数表达式为y=x2-4x+3;
∴y=x2-4x+3=(x-2)2-1,
∴抛物线的顶点坐标为(2,-1),
∴PP′=1,
阴影部分的面积等于平行四边形A′APP′的面积,
平行四边形A′APP′的面积=1×2=2,
∴阴影部分的面积=2.
故答案是:2.
点评 本题考查了待定系数法求二次函数解析式,二次函数的性质,二次函数图象与几何变换,根据平移的性质,把阴影部分的面积转化为平行四边形的面积是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
9.以下说法正确的是( )
| A. | 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是$\frac{3}{10}$ | |
| B. | 随机抛掷一枚均匀的硬币,落地后反面一定朝上 | |
| C. | 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖 | |
| D. | 在一次课堂进行的抛硬币试验中,同学们估计硬币落地后正面朝上的概率为0.51 |
9.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | (2ab)3=6a3b3 | C. | x2•x3=x6 | D. | (a3)2=a6 |
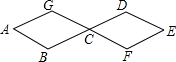 蜜蜂采蜜时,如果蜜源很远它就会跳起“8字舞”,告诉同伴蜜源的方向.如图所示,两个全等菱形的边长为1厘米,一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,飞行2015厘米后停下,则这只蜜蜂停在G点.
蜜蜂采蜜时,如果蜜源很远它就会跳起“8字舞”,告诉同伴蜜源的方向.如图所示,两个全等菱形的边长为1厘米,一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,飞行2015厘米后停下,则这只蜜蜂停在G点.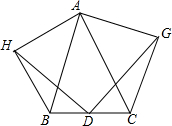 如图,以△ABC中AB,AC为边,向形外作等腰直角三角形ABH和ACG,D为BC边上中点,求证:DG=GH,且DG⊥DH.
如图,以△ABC中AB,AC为边,向形外作等腰直角三角形ABH和ACG,D为BC边上中点,求证:DG=GH,且DG⊥DH.