如图.AD∥BC.BE平分∠ABC.∠BED=145°.则∠BAD=110°．题目和参考答案——青夏教育精英家教网—

题目内容

12．

如图，AD∥BC，BE平分∠ABC，∠BED=145°，则∠BAD=110°．

分析首先根据邻补角的定义求得∠AEB=35°，然后根据平行线的性质可求得∠EBC=35°，接下来根据角平分线的定义可知∠ABE=35°，最后根据三角形的内角和定义即可求得∠EAB的度数．

解答解：∵∠BED=145°，
∴∠AEB=35°．
∵AD∥BC，
∴∠EBC=∠AEB=35°．
∵BE平分∠ABC，
∴∠ABE=∠EBC=35°．
∴∠EAB=180°-∠ABE-∠AEB=180°-35°-35°=110°．

点评本题主要考查的是平行线的性质、角平分线的定义和三角形的内角和定理，求得∠EBC、∠ABE的度数是解题的关键．

练习册系列答案

相关题目

2．连续四次抛掷一枚硬币都是正面朝上，则“第五次抛掷正面朝上”是（　　）

3．

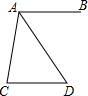如图，AB∥CD，AD平分∠BAC，且∠C=80°，求∠D的度数．

20．如图1，在边长为2的正方形ABCD中，直角∠MAN的两边AM，AN重叠在正方形的两邻边上，现将直角∠MAN绕顶点A逆时针旋转α度（0＜α＜90）．

（1）如图2，在旋转过程中，将正方形的中心O到AM、AN的距离分别记为x、y，则下列各式的值是确定的有④（填序号）
①x+y ②|x-y|③xy ④x²+y²
（2）①如图3，当0＜α＜45时，AM、AN与BC、CD的延长线分别相交于点E、F，求证：BE=DF；
②如图4，当45＜α＜90时，AM、AN与BC、CD的延长线分别相交于点E、F，AM与CD相交于点P，求△APF与△CPE面积的差．
（3）①如图5，当0＜α＜45时，AM、AN与直线BD分别相交于点G、H，求证：$\frac{BG}{DH}$=$\frac{AG}{AH}$；
②如图6，当45＜α＜90时，AM、AN的反向延长线与直线BD分别相交于点G，①中的结论还成立吗？请直接作出判断，不用说明理由．

7．

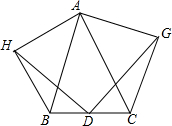如图，以△ABC中AB，AC为边，向形外作等腰直角三角形ABH和ACG，D为BC边上中点，求证：DG=GH，且DG⊥DH．

17．

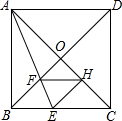如图，在正方形ABCD中，对角线AC，BD交于点O，折叠正方形ABCD，使AB边落在AC上，点B落在点H处，折痕AE分别交BC于点E，交BO于点F，连结FH，则下列结论正确的有几个（　　）
（1）AD=DF；（2）$\frac{{S}_{△ABE}}{S△ACE}$=$\frac{AB}{AC}$；（3）$\frac{FH}{AD}$=$\sqrt{2}$-1；（4）四边形BEHF为菱形．

4．定义一种对正整数n的“F运算”：①当n为奇数时，结果为3n+5；②当n为偶数时，结果为$\frac{n}{{2}^{k}}$（其中k是使$\frac{n}{{2}^{k}}$为奇数的正整数），并且运算重复进行．例如，取n=18时，则：

若n=31，则第31次“F运算”的结果是1．

1．生物学家研究发现，很多植物的生长都有下面的规律，即主干长出若干数目的支干，每个支干又长出同样数目的小分支，某种植物主干、支干和小分支的总数是42，求每个支干长出多少小分支？

2．若x，y为实数，且|x+2|+$\sqrt{y-2}$=0，则（$\frac{x}{y}$）²⁰¹⁵的值为（　　）

试题分类