题目内容
14.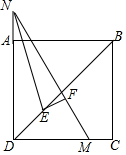 如图所示,正方形ABCD中,M在CD上,N在DA延长线上,CM=AN,点E在BD上,EN平分∠DNM,EF⊥MN于点F,问MN,AD,EF有什么数量关系?
如图所示,正方形ABCD中,M在CD上,N在DA延长线上,CM=AN,点E在BD上,EN平分∠DNM,EF⊥MN于点F,问MN,AD,EF有什么数量关系?
分析 结论:MN=2AD-2EF.作EG⊥AD于G,EH⊥CD于H.由Rt△ENG≌Rt△ENF,Rt△EMH≌Rt△EMF,推出NF=NG,MF=MH,推出MN=NF+FM=NG+MH=DN-DG+DM-DH=AD+AN-DG+DC-CM-DH=2AD-2EF.
解答 解:结论:MN=2AD-2EF.
理由:作EG⊥AD于G,EH⊥CD于H.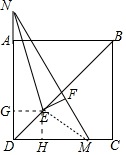
∵四边形ABCD是正方形,
∵AD=CD,∠ADB=∠BDC,∵EG⊥AD,EH⊥DC,
∴EG=EH,
∵∠END=∠ENM,
∴EG=EF,
∴EG=EH=EF,∵EN=EN,EM=EM,
∴Rt△ENG≌Rt△ENF,Rt△EMH≌Rt△EMF,
∴NF=NG,MF=MH,
∵AN=CM,
∴MN=NF+FM=NG+MH=DN-DG+DM-DH=AD+AN-DG+DC-CM-DH=2AD-2EF.
点评 本题考查正方形的性质、全等三角形的判定和性质.角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.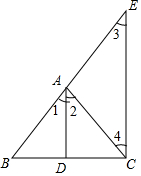 如图,∠1=∠2,EC∥AD.
如图,∠1=∠2,EC∥AD.
求证:∠3=∠4.
证明:∵EC∥AD,
∴∠1=∠3(两直线平行,同位角相等),
∠2=∠4(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠3=∠4(等量代换).
 如图,∠1=∠2,EC∥AD.
如图,∠1=∠2,EC∥AD.求证:∠3=∠4.
证明:∵EC∥AD,
∴∠1=∠3(两直线平行,同位角相等),
∠2=∠4(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠3=∠4(等量代换).
5.下列说法正确的是( )
| A. | 四边形的对角线互相平分 | |
| B. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| C. | 线段的垂直平分线上的点到线段两个端点的距离相等 | |
| D. | 两边对应成比例且有一个角对应相等的两个三角形相似 |
2.一次函数y=-(m2+1)x-(m2+2)的图象(m为常数)不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9. 如图,点D、E、F分别是AB、BC、CA的中点,则图中平行四边形一共有( )
如图,点D、E、F分别是AB、BC、CA的中点,则图中平行四边形一共有( )
 如图,点D、E、F分别是AB、BC、CA的中点,则图中平行四边形一共有( )
如图,点D、E、F分别是AB、BC、CA的中点,则图中平行四边形一共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列函数经过一、二、四象限的是( )
| A. | y=2x+1 | B. | y=-2x+1 | C. | y=2x-1 | D. | y=-2x-1 |
 已知:如图,用长为18m的篱笆(3AB+BC),围成矩形花圃.一面利用墙(墙足够长),则围成的矩形花圃ABCD的占地面积最大为27m2.
已知:如图,用长为18m的篱笆(3AB+BC),围成矩形花圃.一面利用墙(墙足够长),则围成的矩形花圃ABCD的占地面积最大为27m2. 某互联网公司对用户实行两种收费方式:
某互联网公司对用户实行两种收费方式: