题目内容
13.阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,所以a-2$\sqrt{ab}$+b≥0,从而a+b≥2$\sqrt{ab}$(当a=b时取等号).阅读2:函数y=x+$\frac{m}{x}$(常数m>0,x>0),由阅读1结论可知:x+$\frac{m}{x}$≥2$\sqrt{x•\frac{m}{x}}$=2$\sqrt{m}$,所以当x=$\frac{m}{x}$即x=$\sqrt{m}$时,函数y=x+$\frac{m}{x}$的最小值为2$\sqrt{m}$.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为$\frac{4}{x}$,周长为2(x+$\frac{4}{x}$),求当x=2时,周长的最小值为8.
问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),
当x=3时,$\frac{{y}_{2}}{{y}_{1}}$的最小值为8.
问题3:某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
分析 问题1:利用题中的不等式得到x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,从而得到x=2时,周长的最小值为8;
问题2:先变形得到$\frac{{y}_{2}}{{y}_{1}}$=$\frac{(x+1)^{2}+16}{x+1}$=x+1+$\frac{16}{x+1}$,然后利用题中的不等式性质解决问题;
问题3:设学校学生人数为x人,生均投入为y元,依题意得y=$\frac{6400+10x+0.01{x}^{2}}{x}$,变形得到y=$\frac{x}{100}$+$\frac{6400}{x}$+10,然后利用不等式的性质求解.
解答 解:问题1:∵x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,当x=$\frac{4}{x}$时,2(x+$\frac{4}{x}$)有最小值8,
即x=2时,周长的最小值为8;
问题2:$\frac{{y}_{2}}{{y}_{1}}$=$\frac{(x+1)^{2}+16}{x+1}$=x+1+$\frac{16}{x+1}$,
∵x+1+$\frac{16}{x+1}$≥2$\sqrt{(x+1)•\frac{16}{x+1}}$=8,即x+1=$\frac{16}{x+1}$时,$\frac{{y}_{2}}{{y}_{1}}$有最小值,即x=3时,$\frac{{y}_{2}}{{y}_{1}}$的最小值为8;
故答案为2,8;3,8;
问题3:设学校学生人数为x人,生均投入为y元,依题意得:
y=$\frac{6400+10x+0.01{x}^{2}}{x}$=$\frac{x}{100}$+$\frac{6400}{x}$+10,
∵x>0,
∴y=$\frac{x}{100}$+$\frac{6400}{x}$+10=$\frac{1}{100}$(x+$\frac{640000}{x}$)+10≥$\frac{2}{100}$$\sqrt{640000}$+10=16+10,
∴当x=$\frac{640000}{x}$,即x=800时,即x=800时,y取最小值26.
答:当学校学生人数为800人时,该校每天生均投入最低,最低费用是26元.
点评 本题考查了二次函数的应用:几何图形中的二次函数问题常见的有:几何图形中面积的最值,用料的最佳方案以及动态几何中的最值的讨论.也考查了阅读理解能力.

 名校课堂系列答案
名校课堂系列答案| A. | a2+a3=a5 | B. | a•a3=a4 | C. | (ab)4=ab4 | D. | (a3)3=a6 |
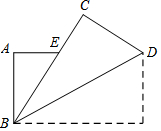 如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:
如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法: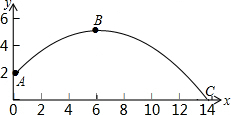 九年级的一名男生在体育课上测试推实心球成绩,已知实心球所经过的路线是某二次函数图象的一部分,如图所示.若这个男生出手处A点的坐标为(0,2),实心球路线的最高处B点的坐标为B(6,5).
九年级的一名男生在体育课上测试推实心球成绩,已知实心球所经过的路线是某二次函数图象的一部分,如图所示.若这个男生出手处A点的坐标为(0,2),实心球路线的最高处B点的坐标为B(6,5).