题目内容
2.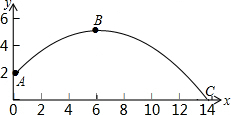 九年级的一名男生在体育课上测试推实心球成绩,已知实心球所经过的路线是某二次函数图象的一部分,如图所示.若这个男生出手处A点的坐标为(0,2),实心球路线的最高处B点的坐标为B(6,5).
九年级的一名男生在体育课上测试推实心球成绩,已知实心球所经过的路线是某二次函数图象的一部分,如图所示.若这个男生出手处A点的坐标为(0,2),实心球路线的最高处B点的坐标为B(6,5).(1)求这个二次函数的表达式;
(2)问该男生把实心球推出去多远?(结果保留根号)
分析 (1)根据抛物线的顶点坐标,设其顶点式,由A坐标可得答案;
(2)令y=0,解方程求得x的值即可.
解答 解:(1)设抛物线解析式为y=a(x-6)2+5(a≠0),
∵A(0,2)在抛物线上,
∴代入得a=-$\frac{1}{12}$,
∴抛物线的解析式为y=-$\frac{1}{12}$(x-6)2+5.
(2)∵令y=0,即-$\frac{1}{12}$(x-6)2+5=0,解得x1=6-2$\sqrt{15}$(舍去),x2=6+2$\sqrt{15}$
∴OC=6+2$\sqrt{15}$.
答:该同学把实心球扔出(6+2$\sqrt{15}$)m.
点评 本题考查的是二次函数的应用,熟知利用待定系数法求二次函数的解析式是解答此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目




 如图,点E为矩形ABCD外一点,AE=DE,连接EB、EC分别与AD相交于点F、G.求证:BE=CE.
如图,点E为矩形ABCD外一点,AE=DE,连接EB、EC分别与AD相交于点F、G.求证:BE=CE. 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数46°.
如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数46°.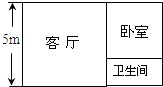 如图,有一长方形的仓库,一边长为5m,现要将它改建为简易住房,改建后的住房分为客厅、卧室和卫生间三部分,其中客厅和卧室都为正方形,且卧室的面积大于卫生间的面积,若改建后卫生间的面积为6m2,则长方形仓库另一边的长是8m.
如图,有一长方形的仓库,一边长为5m,现要将它改建为简易住房,改建后的住房分为客厅、卧室和卫生间三部分,其中客厅和卧室都为正方形,且卧室的面积大于卫生间的面积,若改建后卫生间的面积为6m2,则长方形仓库另一边的长是8m.