题目内容
17．已知二次函数y=ax2+bx+c的图象过（-1，3），（1，1）两点且它与y轴交点的纵坐标大于0且小于1，则a的取值范围是（ ）| A． | 1＜a＜3 | B． | 1≤a≤3 | C． | 2≤a＜3 | D． | 1＜a＜2 |
分析 将（-1，3），（1，1）分别代入二次函数y=ax2+bx+c，得出b=-1，c=2-a，当x=0时，y=c，故0＜2-a＜1，进一步解不等式组得出答案即可．
解答 解：将（-1，3），（1，1）分别代入二次函数y=ax2+bx+c，得
$\left\{\begin{array}{l}{a-b+c=3}\\{a+b+c=1}\end{array}\right.$，
解得：b=-1，c=2-a，
∵当x=0时，y=c，
∴0＜2-a＜1，
解得：1＜a＜2．
故选：D．
点评 此题考查二次函数的性质，利用待定系数法求得a、c的关系是解决问题的关键．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
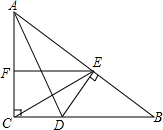如图．在Rt△ABC中．已知∠C=90°，AD平分∠BAC，点D在BC上，DE⊥AB，垂足为E，EF∥BC．求证：EC平分∠FED．