题目内容
2.某水产店每天购进一种高档海鲜500千克,预计每千克盈利10元,当天可全部售完,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克,当天剩余的海鲜全部以每千克盈利5元的售价卖给某饭店,那么每千克应涨价多少元,可以获得最大利润,最大利润是多少?分析 设每千克应涨价x元,根据总利润=涨价利润后的利润+剩余的销售利润列出方程探讨得出答案即可.
解答 解:设每千克应涨价x元,每天的盈利为y,由题意,得
y=(10+x)(500-20x)+5×20x,
整理,得y=-20x2+400x+5000=-20(x-10)2+7000,
即:当x=10元时,y最大=7000元.
答:每千克应涨价10元,可以获得最大利润,最大利润是7000元.
点评 本题考查的是二次函数的应用,一元二次方程的应用,根据题意列出关于x的一元二次方程是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知二次函数y=ax2+bx+c的图象过(-1,3),(1,1)两点且它与y轴交点的纵坐标大于0且小于1,则a的取值范围是( )
| A. | 1<a<3 | B. | 1≤a≤3 | C. | 2≤a<3 | D. | 1<a<2 |
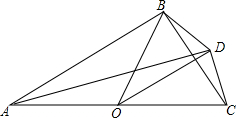 如图,OA=OB=OD=OC=3,且∠BAD=15°,则S△BOD=$\frac{9}{4}$.
如图,OA=OB=OD=OC=3,且∠BAD=15°,则S△BOD=$\frac{9}{4}$.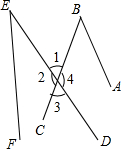 如图:
如图: