题目内容
7.已知一次函数y=(a+1)x+b-2(1)若y随x的增大而减少,图象与x轴的负半轴交于一点,求a、b的取值范围;
(2)若b=2a-1,函数图象不经过第二象限,求a的取值范围.
分析 (1)根据一次函数图象的性质y随x的增大而减少得出a+1<0,和图象与x轴的负半轴交于一点得出$\frac{b-2}{a+1}<0$解答即可;
(2)根据函数图象不经过第二象限得出a+1>0进行解答.
解答 解:(1)因为y随x的增大而减少,图象与x轴的负半轴交于一点,
可得:a+1<0,$\frac{b-2}{a+1}<0$,
可得:a<-1,b>2;
(2)因为b=2a-1,函数图象不经过第二象限,
可得:a+1>0,b-2<0,
解得:$-1<a<\frac{3}{2}$.
点评 主要考查一次函数图象的性质,关键是根据一次函数图象的性质符合要求得出不等式解答.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
17.已知二次函数y=ax2+bx+c的图象过(-1,3),(1,1)两点且它与y轴交点的纵坐标大于0且小于1,则a的取值范围是( )
| A. | 1<a<3 | B. | 1≤a≤3 | C. | 2≤a<3 | D. | 1<a<2 |
20.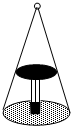 如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )
如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )
 如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )
如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )| A. | 0.36π米2 | B. | 0.81π米2 | C. | 2π米2 | D. | 3.24π米2 |