题目内容
7.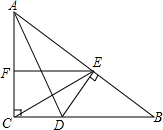 如图.在Rt△ABC中.已知∠C=90°,AD平分∠BAC,点D在BC上,DE⊥AB,垂足为E,EF∥BC.求证:EC平分∠FED.
如图.在Rt△ABC中.已知∠C=90°,AD平分∠BAC,点D在BC上,DE⊥AB,垂足为E,EF∥BC.求证:EC平分∠FED.
分析 根据角平分线的性质得到DE=DC,根据等腰三角形的性质得到∠DCE=∠DEC,根据平行线的性质和等量代换证明即可.
解答 证明:∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=DC,
∴∠DCE=∠DEC,
∵EF∥BC,
∴∠DCE=∠FEC,
∴∠FEE=∠DEC,
∴EC平分∠FED.
点评 本题考查的是角平分线的性质和平行线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知二次函数y=ax2+bx+c的图象过(-1,3),(1,1)两点且它与y轴交点的纵坐标大于0且小于1,则a的取值范围是( )
| A. | 1<a<3 | B. | 1≤a≤3 | C. | 2≤a<3 | D. | 1<a<2 |
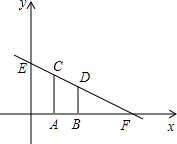 在平面直角坐标系中,CA⊥x轴于点A(1,0),BD⊥x轴于点B(3,0),直线CD与x轴,y轴分别交于点F,E,且解析式y=kx+3,S四边形ABCD=4,求直线CD的解析式.
在平面直角坐标系中,CA⊥x轴于点A(1,0),BD⊥x轴于点B(3,0),直线CD与x轴,y轴分别交于点F,E,且解析式y=kx+3,S四边形ABCD=4,求直线CD的解析式.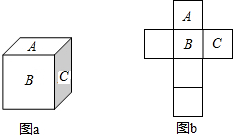 如图,正方体a的上、前、右三个面上分别注有A,B,C三个字母,它的展开图如图b所示,请用D,E,F,三个字母在展开图上分别标注下、后、左三个面.
如图,正方体a的上、前、右三个面上分别注有A,B,C三个字母,它的展开图如图b所示,请用D,E,F,三个字母在展开图上分别标注下、后、左三个面.