题目内容
8.如果x3m+2ny2n+1÷x2ym=x3y2,则m+n的平方根是$±\sqrt{2}$.分析 根据整式的除法得出m和n的值,再得出代数式解答即可.
解答 解:因为x3m+2ny2n+1÷x2ym=x3y2,
所以可得:$\left\{\begin{array}{l}{3m+2n-2=3}\\{2n+1-m=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=1}\\{n=1}\end{array}\right.$.
所以m+n的平方根是$±\sqrt{2}$,
故答案为:$±\sqrt{2}$.
点评 此题考查整式的除法问题,关键是根据整式的除法得出m和n的值.

练习册系列答案
相关题目
20.把抛物线y=-2(x-1)2+1的图象向左平移3个单位,再向下平移4个单位,所得的抛物线的函数关系式是( )
| A. | y=-2(x+2)2-3 | B. | y=-2(x-4)2-3 | C. | y=2(x+2)2-6D | D. | y=-2(x-4)2+5 |
17.已知二次函数y=ax2+bx+c的图象过(-1,3),(1,1)两点且它与y轴交点的纵坐标大于0且小于1,则a的取值范围是( )
| A. | 1<a<3 | B. | 1≤a≤3 | C. | 2≤a<3 | D. | 1<a<2 |
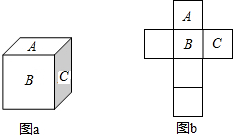 如图,正方体a的上、前、右三个面上分别注有A,B,C三个字母,它的展开图如图b所示,请用D,E,F,三个字母在展开图上分别标注下、后、左三个面.
如图,正方体a的上、前、右三个面上分别注有A,B,C三个字母,它的展开图如图b所示,请用D,E,F,三个字母在展开图上分别标注下、后、左三个面.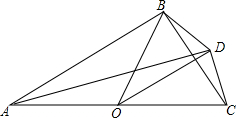 如图,OA=OB=OD=OC=3,且∠BAD=15°,则S△BOD=$\frac{9}{4}$.
如图,OA=OB=OD=OC=3,且∠BAD=15°,则S△BOD=$\frac{9}{4}$.