题目内容
10.设抛物线为y=x2-kx+k-1,y的最小值为-1,求k的值.分析 先把一般式配成顶点式得到y=(x-$\frac{k}{2}$)2+$\frac{3}{4}$k-1,利用二次函数的最值问题得到当x=$\frac{k}{2}$时,y有最小值,于是$\frac{k}{2}$=-1,然后解关于k的方程即可.
解答 解:y=x2-kx+k-1=(x-$\frac{k}{2}$)2+$\frac{3}{4}$k-1,
当x=$\frac{k}{2}$时,y有最小值,最小值为$\frac{3}{4}$k-1,
所以$\frac{k}{2}$=-1,
所以k=-2.
点评 本题考查了二次函数的最值:确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.
如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.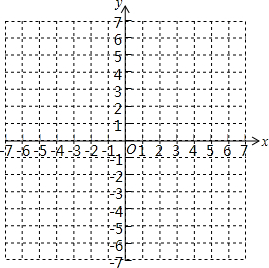 在图中画出函数y=-x+1,y=2x-5的图象,利用图象回答下列问题:
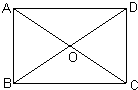
在图中画出函数y=-x+1,y=2x-5的图象,利用图象回答下列问题: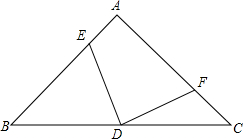 如图,已知等腰直角三角形△ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF.求证:DE=DF;DE⊥DF.
如图,已知等腰直角三角形△ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF.求证:DE=DF;DE⊥DF.

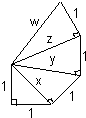 x=$\sqrt{2}$,y=$\sqrt{3}$,z=2,w=$\sqrt{5}$.
x=$\sqrt{2}$,y=$\sqrt{3}$,z=2,w=$\sqrt{5}$.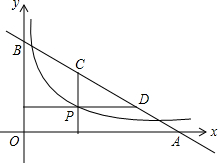 如图,P是函数y=$\frac{\sqrt{3}}{x}$(x>0)图象上的一点,直线y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与x轴、y轴别交于A,B两点,过P作x轴、y轴的垂线与该直线分别交于C,D两点,则AD•BC=4.
如图,P是函数y=$\frac{\sqrt{3}}{x}$(x>0)图象上的一点,直线y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与x轴、y轴别交于A,B两点,过P作x轴、y轴的垂线与该直线分别交于C,D两点,则AD•BC=4.