题目内容

1．已知在△ABC中，a2-16b2-c2+6ab+10bc=0（a、b、c是三角形三边的长）．求证：a+c=2b．

分析 通过配方，开平方得出a+c=2b或a+8b=c，再由三角形的三边关系即可得出结论．

解答 证明：a2-16b2-c2+6ab+10bc=0，
配方得：（a+3b）2=（5b-c）2，
开平方得：a+3b=±（5b-c），
解得：a+c=2b或a+8b=c，
∵在△ABC中，a-c＜b，
∴a+8b=c不合题意，舍去；
∴a+c=2b．

点评 本题考查了配方法、开平方、提取公因式法、平方差公式因式分解．熟练掌握配方法和因式分解的方法，解决问题．

练习册系列答案
相关题目
4．已知：如图，四边形BCDE是矩形，AB=AC，求证：AE=AD．
5．已知抛物线y=a（x-h）2-2（a，h，是常数，a≠0），x轴交于点A，B，与y轴交于点C，点M为抛物线顶点．
（Ⅰ）若点A（-1，0），B（5，0），求抛物线的解析式；
（Ⅱ）若点A（-1，0），且△ABM是直角三角形，求抛物线的解析式；
（Ⅲ）若抛物线与直线y1=x-6相交于M、D两点
①用含a的式子表示点D的坐标；
②当CD∥x轴时，求抛物线的解析式．
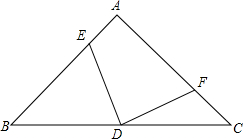2．如图，已知等腰直角三角形△ABC中，∠A=90°，D为BC中点，E、F分别为AB、AC上的点，且满足EA=CF．求证：DE=DF；DE⊥DF．
9．若一元二次方程（x-3）2=m-1没有实数根，则m的取值范围为m＜1．
6．“双基”考查题（每题2分，共30分）
（1）-27的立方根是-3，18的算术平方根是3$\sqrt{2}$．
（2）化简：$\sqrt{3}×\sqrt{\frac{25}{48}}$=$\frac{5}{4}$，$\sqrt{18}-3\sqrt{32}$=-9$\sqrt{2}$．
（3）比较大小：$\frac{{\sqrt{5}-1}}{2}$＜ $\frac{7}{8}$，$\sqrt{32}$＜5.6．
（4）图象经过点A（-2，6）的正比例函数的关系式为y=-3x．
（5）方程组$\left\{\begin{array}{l}x+2y=7\\ x-2y=3\end{array}\right.$的解是$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$．
（6）八年级一班47名同学中，12岁的有5人，13岁的有27人，14岁的有12人，15岁的有3人，则这班同学的年龄的众数是13岁，中位数是13岁．
（7）一个正多边形的每个内角都为135°，则这个多边形的内角和是1080度．

（8）将一条2cm线段向右平移3cm后，连接对应点得到的图形的周长是10cm．
（9）、某拖拉机的油箱有油100升，每工作1小时耗油8升，则油箱的剩余油量y（升）与工作时间x（时）间的函数关系式为y=-8x+100．
（10）如图，正方形ABCD的对角线相交于点O，这个正方形可以看作由什么“基本图形”经过怎样的变化形成的？Rt△ABC轴对称得到．
（11）如图是用形状、大小完全相同的等腰梯形密铺成的图案的一部分，这个图案中的等腰梯形的内角度数分别是60°，60°120°，120°．
（12）如图，若用（2，3）表示图上校门A的位置，则图书馆B的位置可表示为（1，6），（5，5）表示点D的位置．
（13）如图，矩形ABCD的对角线AC、BD相交于点O，∠AOB=60°，AB=4cm，则△AOB的形状是等边三角形，AC长是8cm，BC长是4$\sqrt{3}$cm．
（14）小明从九龙山邮局买了面值50分和80分的邮票共9枚，花了6.3元．小明买了两种邮票各多少枚？
若设买了面值50分的邮票x枚，80分的邮票y枚，则可列出的方程组是$\left\{\begin{array}{l}{x+y=9}\\{0.5x+0.8y=6.3}\end{array}\right.$．
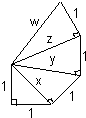（15）根据图填空：x=$\sqrt{2}$，y=$\sqrt{3}$，z=2，w=$\sqrt{5}$．
13．如图1，已知△ABC中，∠C=90°，AC=6，BC=8，点E，F在AC，BC上，将△ABC沿EF折叠，点C落在点D处，设△EDF与四边形ABFE重叠部分面积为y，CF长为x．

（1）如图2，当EF∥AB，CF=4时，试求y的值；
（2）当EF∥AB时，试求y与x的函数关系式，并求x为何值时y的值最大；
（3）如图3，当CF=4，DF⊥BC时，求y的值．
10．（1）若125x3+27=0，求x的值；
（2）若25y2-36=0，求y的值．
11．计算或化简（整式乘法）
（1）（-3ab）•（-4b）2
（2）（$\frac{4}{3}$×105）•（9×103）2
（3）3x（x2-2x-1）+6x
（4）（x+5）（x-2）+（-x+1）（x-2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网