题目内容
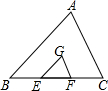 如图,点G是△ABC的重心,过G作CG∥AB,交BC于点E,GF∥AC,交AB于点F,则S△GEF:S△ABC=
如图,点G是△ABC的重心,过G作CG∥AB,交BC于点E,GF∥AC,交AB于点F,则S△GEF:S△ABC=考点:三角形的重心
专题:计算题
分析:连结AG,并延长交BC于H,如图,根据三角形重心的性质得到HG=
AG,则HG=
HA,再由EG∥AB得到△HGE∽△HAB,根据相似三角形的性质得
=
=
,接着证明△GEF∽△ABC,然后利用相似三角形的性质求
的值.
| 1 |
| 2 |
| 1 |
| 3 |
| GE |
| AB |
| HG |
| HA |
| 1 |
| 3 |
| S△GEF |
| S△ABC |
解答:解:连结AG,并延长交BC于H,如图,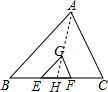
∵点G是△ABC的重心,
∴HG=
AG,
∴HG=
HA,
∵EG∥AB,
∴△HGE∽△HAB,
∴
=
=
,
∵EG∥AB,GF∥AC,
∴∠GEF=∠B,∠GFE=∠C,
∴△GEF∽△ABC,
∴
=(
)2=(
)2=
.
故答案为1:9.

∵点G是△ABC的重心,
∴HG=
| 1 |
| 2 |
∴HG=
| 1 |
| 3 |
∵EG∥AB,
∴△HGE∽△HAB,
∴
| GE |
| AB |
| HG |
| HA |
| 1 |
| 3 |
∵EG∥AB,GF∥AC,
∴∠GEF=∠B,∠GFE=∠C,
∴△GEF∽△ABC,
∴
| S△GEF |
| S△ABC |
| GE |
| AB |
| 1 |
| 3 |
| 1 |
| 9 |
故答案为1:9.
点评:本题考查了三角形的重心:三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
某小组同学聚会,见面时相互间均握了一次手,好事者统计:一共握了36次.你认为这次聚会的同学有( )人.
| A、7 | B、8 | C、9 | D、10 |
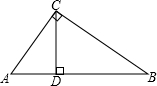 在Rt△ABC中,∠C=90°,BC=8,S△ABC=24,求斜边AB上的高.
在Rt△ABC中,∠C=90°,BC=8,S△ABC=24,求斜边AB上的高.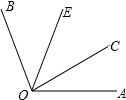 如图,OC是∠AOB内部的一条射线,∠AOC=32°,OE是∠COB的平分线.已知∠COE=43°,则∠AOB=
如图,OC是∠AOB内部的一条射线,∠AOC=32°,OE是∠COB的平分线.已知∠COE=43°,则∠AOB= 如图,在Rt△ACB中,∠ACB=90°,点D是AB上一点.将△BCD沿CD折叠,使B点落在AC边上的B′处.
如图,在Rt△ACB中,∠ACB=90°,点D是AB上一点.将△BCD沿CD折叠,使B点落在AC边上的B′处.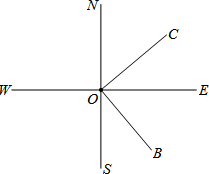 如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余. 如图是某个几何体的表面展开图,那么这个几何体是
如图是某个几何体的表面展开图,那么这个几何体是