题目内容
14.如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED=60°
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1,l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).
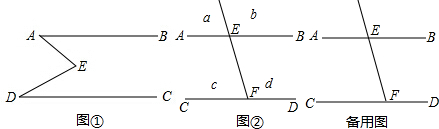
分析 (1)①过E作EF∥AB,根据AB∥CD,可得AB∥EF∥CD,再根据两直线平行,内错角相等进行计算即可;
②作辅助线构造内错角,依据两直线平行,内错角相等或三角形外角性质,进行计算即可;
(2)根据a,b,c,d分别是被射线FE隔开的4个区域,P是位于四个区域上的点,画出对应的图形,进而得出结论.
解答 解:(1)①过E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠A=∠AEF=20°,∠D=∠DEF=40°,
∴∠AED=∠AEF+∠DEF=∠A+∠D=60°,
故答案为:60;
②∠AED=∠A+∠D,
证明:方法一、延长DE交AB于F,如图1,
∵AB∥CD,
∴∠DFA=∠D,
∴∠AED=∠A+∠DFA;
方法二、过E作EF∥AB,如图2,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠A=∠AEF,∠D=∠DEF,
∴∠AED=∠AEF+∠DEF=∠A+∠D;
(2)当P在a区域时,如图3,∠PEB=∠PFC+∠EPF;
当P点在b区域时,如图4,∠PFC=∠PEB+∠EPF;
当P点在区域c时,如图5,∠EPF+∠PEB+∠PFC=360°;
当P点在区域d时,如图6,∠EPF=∠PEB+∠PFC.
点评 本题主要考查了平行线的性质,以及三角形外角性质,解题时注意:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
4.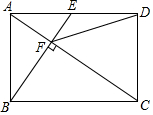 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.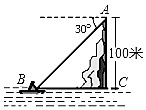 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )| A. | 50$\sqrt{3}$ | B. | 100 | C. | 100+$\sqrt{3}$ | D. | 100$\sqrt{3}$ |
9.下列不能进行平方差计算的是( )
| A. | (x+y)(-x-y) | B. | (2a+b)(2a-b) | C. | (-3x-y)(-y+3x) | D. | (a2+b)(a2-b) |
19.如图(1)是两圆柱形联通容器(联通外体积忽略不计).向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲的底面半径为1cm,则乙容器底面半径为( )
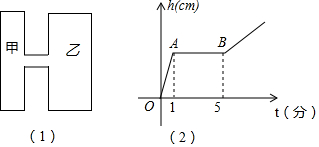

| A. | 5cm | B. | 4cm | C. | 3cm | D. | 2cm |
4.若等腰三角形中有两边长分别为3和7,则这个三角形的周长为( )
| A. | 13 | B. | 17 | C. | 10或13 | D. | 13或17 |
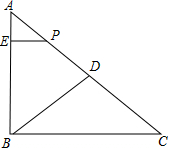 如图,在Rt△ABC中,∠ABC=90°,AC=10cm,BC=8cm,点D是线段AC的中点,动点P从点A出发,沿A-D-B-C向终点C运动,速度为5cm/s,当点P不与点A,B重合时,作PE⊥AB交线段AB于点E,设点P的运动时间为t(s),△APE的面积为S(cm2).
如图,在Rt△ABC中,∠ABC=90°,AC=10cm,BC=8cm,点D是线段AC的中点,动点P从点A出发,沿A-D-B-C向终点C运动,速度为5cm/s,当点P不与点A,B重合时,作PE⊥AB交线段AB于点E,设点P的运动时间为t(s),△APE的面积为S(cm2).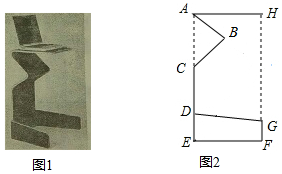 如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°.
如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后楼梯AC长为2$\sqrt{6}$米.
如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后楼梯AC长为2$\sqrt{6}$米.