题目内容
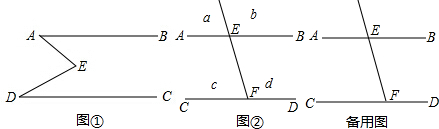
3. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后楼梯AC长为2$\sqrt{6}$米.
如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后楼梯AC长为2$\sqrt{6}$米.
分析 先在Rt△ABD中利用正弦的定义计算出AD,然后在Rt△ACD中利用正弦的定义计算AC即可.
解答 解:在Rt△ABD中,∵sin∠ABD=$\frac{AD}{AB}$,
∴AD=4sin60°=2$\sqrt{3}$(m),
在Rt△ACD中,∵sin∠ACD=$\frac{AD}{AC}$,
∴AC=$\frac{2\sqrt{3}}{sin45°}$=2$\sqrt{6}$(m).
故答案是:2$\sqrt{6}$.
点评 本题考查了解直角三角形的实际应用中的坡度坡角问题,难度不大,注意细心运算即可.

练习册系列答案
相关题目
13.下列各选项的图形中,中心对称图形是( )
| A. |  | B. |  | C. |  | D. |  |
11.下列计算中,正确的是( )
| A. | (m-2)(m+2)=m2-2 | B. | (x-6)(x+6)=x2+36 | C. | (x-y)(x+y)=x2-y2 | D. | (x+y)(x+y)=x2+y2 |
18.唐山是中国第一个承办世界园艺博览会的地市级城市,绿化总面积140万平方米,数据140万用科学记数法表示为( )
| A. | 14×104 | B. | 1.4×102 | C. | 14×105 | D. | 1.4×106 |
15.若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点(2,1),则这个函数的图象还经过的点是( )
| A. | (-2,1) | B. | (-l,2) | C. | (-2,-1) | D. | (1,-2) |
13.函数y=$\sqrt{x+1}$中自变量x的取值范围是( )
| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |