题目内容
19.已知x=$\sqrt{2}$-1,则4x2+8x-7的值为-3.分析 先变形已知条件得到x2+2x=1,再变形4x2+8x-7得到4(x2+2x)-7,然后利用整体代入的方法计算.
解答 解:∵x=$\sqrt{2}$-1,
∴x+1=$\sqrt{2}$,
∴(x+1)2=2,
∴x2+2x=1,
∴4x2+8x-7=4(x2+2x)-7=4×1-7=-3.
故答案为-3.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
14.如图,在平面直角坐标系中,用描点法分别画出函数y=-x+1与y=-$\frac{2}{x}$的图象,并写出不等式-x+1>-$\frac{2}{x}$的解集.
解:列表:
画图象:
不等式-x+1>-$\frac{2}{x}$的解集为x<-1或0<x<2.
解:列表:
| x | … | … | ||||||
| y=-x+1 | … | … | ||||||
| y=-$\frac{2}{x}$ | … | … |

不等式-x+1>-$\frac{2}{x}$的解集为x<-1或0<x<2.
11.化简$\sqrt{(m-5)^{2}(5-m)}$的正确结果是( )
| A. | (m-5)$\sqrt{5-m}$ | B. | (5-m)$\sqrt{5-m}$ | C. | m-5$\sqrt{-(5-m)}$ | D. | 5-m$\sqrt{5-m}$ |
8.若1<x<2,则$\sqrt{4-4x+{x}^{2}}$+$\sqrt{{x}^{2}+2x+1}$化简的结果是( )
| A. | 2x-1 | B. | -2x+1 | C. | -3 | D. | 3 |
 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).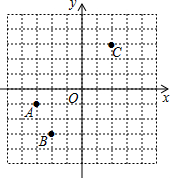 点A,B,C在如图所示的平面直角坐标系内,按要求完成下列各小题.
点A,B,C在如图所示的平面直角坐标系内,按要求完成下列各小题. 如图,矩形ABCD中,点E为AB中点,连接CE,将顶点B沿CE折叠至点P处,连接AP并延长交边CD于点F,
如图,矩形ABCD中,点E为AB中点,连接CE,将顶点B沿CE折叠至点P处,连接AP并延长交边CD于点F,