题目内容
1.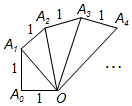 如图是由一系列直角三角形组成的螺旋形,OA0=A0A1=A1A2=…=1,则第n个直角三角形的面积为$\frac{\sqrt{n}}{2}$.
如图是由一系列直角三角形组成的螺旋形,OA0=A0A1=A1A2=…=1,则第n个直角三角形的面积为$\frac{\sqrt{n}}{2}$.
分析 根据题意分别得出直角三角形的面积进而得出答案.
解答 解:∵OA0=A0A1=A1A2=…=1,
∴第1个直角三角形的面积为:$\frac{1}{2}$,
第2个直角三角形的面积为:$\frac{1}{2}$×$\sqrt{2}$×1=$\frac{\sqrt{2}}{2}$,
第3个直角三角形的面积为:$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
…
∴第n个直角三角形的面积为:$\frac{\sqrt{n}}{2}$,
故答案为:$\frac{{\sqrt{n}}}{2}$.
点评 此题主要考查了勾股定理,正确得出三角形面积是解题关键.

练习册系列答案
相关题目
9.已知a,b是一元二次方程x2+2x-9=0的两根,则a2+a-b的值等于( )
| A. | 7 | B. | 11 | C. | -7 | D. | -11 |
10.以下各图中,能确定∠1=∠2的是( )
| A. |  | B. |  | C. |  | D. |  |
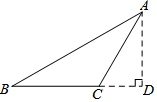 如图,在△ABC中,AB=17,BC=9,AC=10,试求△ABC的面积.
如图,在△ABC中,AB=17,BC=9,AC=10,试求△ABC的面积.