题目内容
11.已知代数式$\frac{ax+b}{x+c}$可以表示为a+$\frac{m}{x+c}$的形式,则m=b-ac.分析 分式的加减运算即可求出答案.
解答 解:a+$\frac{m}{x+c}$
=$\frac{a(x+c)}{x+c}$+$\frac{m}{x+c}$
=$\frac{ax+ac+m}{x+c}$,
∴ac+m=b,
∴m=b-ac
故答案为:b-ac
点评 本题考查分式的加减法,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
2.下列各式中,与分式$\frac{ax+ay}{{x}^{2}-{y}^{2}}$相等的是( )
| A. | $\frac{2a}{x+y}$ | B. | $\frac{a}{x+y}$ | C. | $\frac{2a}{x-y}$ | D. | $\frac{a}{x-y}$ |
19.下列函数中y=-4x,y=$\frac{x}{2}$-3,y=$\frac{x+4}{3}$,y=$\frac{2}{x}$-1,y=-x2+1,y=-2$\sqrt{x}$,y=3,3x+2y=5,其中y是x的一次函数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.下列实数:$\frac{π}{2}$,$\frac{22}{7}$,1.414,$\root{3}{9}$,$\sqrt{\frac{1}{2}}$,2.01010010001…,-$\sqrt{36}$中,无理数有( )个.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
1. 如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
 如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )| A. | $\sqrt{2015}$ | B. | $\sqrt{2016}$ | C. | $\sqrt{2017}$ | D. | $\sqrt{2018}$ |
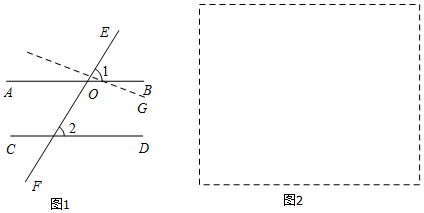
 如图,已知∠1=∠2,∠3=110°,求∠4的度数.
如图,已知∠1=∠2,∠3=110°,求∠4的度数.