题目内容
19.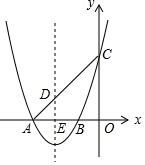 如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C.
如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C.(1)求A、B、C三点的坐标.
(2)求抛物线的对称轴及顶点坐标.
(3)抛物线上是否存在点F,使△ABF的面积为1?若存在,求F点的坐标;若不存在,请说明理由.
分析 (1)根据x2+4x+3=0,解得x1=-3、x2=-1,即点A(-3,0),B(-1,0),根据抛物线y=x2+4x+3交y轴于点C,可知当x=0时,y=3,所以C(0,3);
(2)根据二次函数y=ax2+bx+c的对称轴为x=-$\frac{b}{2a}$,顶点坐标为($-\frac{b}{2a}$,$\frac{4ac{-b}^{2}}{4a}$),求得抛物线的对称轴和顶点坐标;
(3)设出F点的横坐标,纵坐标用横坐标表示,将三角形ABF的面积用F点的横坐标表示出来,等于1,建立方程,解之即可.
解答 解:(1)∵抛物线y=x2+4x+3交x轴于A、B两点,
∴令y=0,则x2+4x+3=0,
解得x1=-3、x2=-1,即点A(-3,0),B(-1,0),
令x=0,则y=3,
∴C(0,3);
(2)对称轴:$-\frac{b}{2a}$=$-\frac{4}{2×1}$=-2;
顶点坐标:x=$-\frac{b}{2a}$=-2,y=$\frac{4ac{-b}^{2}}{4a}$=$\frac{4×1×3{-4}^{2}}{4×1}$=-1;
顶点坐标为(-2,-1);
(3)∵A(-3,0),B(-1,0),
∴AB=2,
设F点坐标为(m,m2+4m+3),
则S△ABF=$\frac{1}{2}×2$×|m2+4m+3|=1,
∴|m2+4m+3|=1,
∴m2+4m+3=1或m2+4m+3=-1,
解得:m=-2+$\sqrt{2}$或m=-2-$\sqrt{2}$或m=-2,
∴点满足要求的点F的坐标为:(-2+$\sqrt{2}$,1)、(-2-$\sqrt{2}$,1)、(-2,-1).
点评 本题考查了待定系数法求二次函数解析式、三角形面积的坐标表示,解一元二次方程等知识点,关键是第(2)问当中,将三角形ABF的高用F点纵坐标的绝对值表示,这样建立方程可一次性解出各个解,避免了分类讨论.

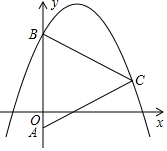 如图,已知抛物线y=-$\frac{2}{3}$x2+$\sqrt{3}$x+3的图象与y轴交于点B,点C是抛物线在第一象限上的一动点,若以BC为边作正△ABC交y轴于点A,则点A的坐标为( )
如图,已知抛物线y=-$\frac{2}{3}$x2+$\sqrt{3}$x+3的图象与y轴交于点B,点C是抛物线在第一象限上的一动点,若以BC为边作正△ABC交y轴于点A,则点A的坐标为( )| A. | (-1,0) | B. | (-$\sqrt{3}$,0) | C. | (0,1) | D. | (0,$\sqrt{3}$) |
| A. | a2nbmn | B. | a${\;}^{{n}^{2}}$b${\;}^{{m}^{n}}$ | C. | a${\;}^{{n}^{2}}$bmn | D. | a2nb${\;}^{{m}^{n}}$ |
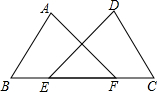 如图,点E、F在线段BC上且F在E的右侧,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
如图,点E、F在线段BC上且F在E的右侧,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.