题目内容
4.一次函数y=ax-a+1(a为常数,且a≠0).(1)若点(-$\frac{1}{2}$,3)在一次函数y=ax-a+1的图象上,求a的值;
(2)求此一次函数与两坐标轴围成的三角形面积.
分析 (1)根据一次函数图象上点的坐标特征把(-$\frac{1}{2}$,3)代入y=ax-a+1中可求出a的值即可;
(2)求出直线与坐标轴的交点,利用三角形的面积公式即可得出结论.
解答 解:(1)把(-$\frac{1}{2}$,3)代入y=ax-a+1得-$\frac{1}{2}$a-a+1=3,解得a=-$\frac{4}{3}$;
(2)∵a=-$\frac{4}{3}$,
∴直线的解析式为:y=-$\frac{4}{3}$x+$\frac{7}{3}$,
∴直线与坐标轴的交点为(0,$\frac{7}{3}$),($\frac{7}{4}$,0),
∴S=$\frac{1}{2}$×$\frac{7}{3}$×$\frac{7}{4}$=$\frac{49}{24}$.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
14.若a、b、c分别表示方程x2+1=3x中的二次项系数、一次项系数和常数项,则a、b、c的值为( )
| A. | a=1,b=-3,c=-1 | B. | a=1,b=-3,c=1 | C. | a=-1,b=-3,c=1 | D. | a=-1,b=3,c=1 |
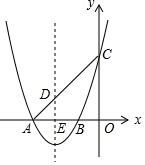 如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C.
如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C.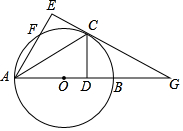 如图,AB是⊙O的直径,C为⊙O上一点,CD垂直AB于D,把△ACD沿直线AC折叠得到△ACE,AE交⊙O于F点,EC、AB的延长线交于G
如图,AB是⊙O的直径,C为⊙O上一点,CD垂直AB于D,把△ACD沿直线AC折叠得到△ACE,AE交⊙O于F点,EC、AB的延长线交于G