题目内容
17.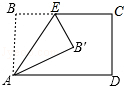 将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=60°,则∠AEB′的正切值=$\sqrt{3}$.
将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=60°,则∠AEB′的正切值=$\sqrt{3}$.
分析 根据折叠的性质,可得出∠AEB′=∠AEB,再由已知∠CEB′=60°,求得∠AEB′=60°,然后根据特殊角的三角函数值即可求解.
解答 解:∵∠AEB′是△AEB沿AE折叠而得,
∴∠AEB′=∠AEB.
又∵∠BEC=180°,即∠AEB′+∠AEB+∠CEB′=180°,
又∵∠CEB′=60°,
∴∠AEB′=$\frac{1}{2}$(180°-∠CEB′)=60°,
∴∠AEB′的正切值=tan60°=$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查了角的计算,折叠问题以及特殊角的三角函数值.图形的折叠实际上相当于把折叠部分沿着折痕所在直线作轴对称,所以折叠前后的两个图形是全等三角形,重合的部分就是对应量.

练习册系列答案
相关题目
7.下列二次根式中,不能再化简的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{0.2}$ |
5.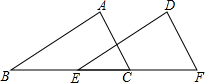 如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
 如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )| A. | BC=EF | B. | ∠ACB=∠F | C. | ∠B=∠DEF | D. | AB=DE |
2.下列计算结果正确的是( )
| A. | (x3)3=x6 | B. | a6•a4=a10 | C. | (ab4)4=ab8 | D. | (-3pq)2=-6p2q2 |
 已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=8,则线段BD+CE的长为( )
已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=8,则线段BD+CE的长为( )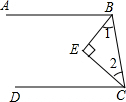 如图,已知BE、CE分别平分∠ABC、∠BCD,且∠1+∠2=90°,求证:AB∥CD.
如图,已知BE、CE分别平分∠ABC、∠BCD,且∠1+∠2=90°,求证:AB∥CD.