题目内容
11.已知x+y=-4,xy=-12,则$\frac{x+1}{y+1}+\frac{y+1}{x+1}$=-$\frac{34}{15}$.分析 先根据分式混合运算的法则把原式进行化简,再把x+y=-4,xy=-12代入进行计算即可.
解答 解:原式=$\frac{(x+1)^{2}+(y+1)^{2}}{(y+1)(x+1)}$
=$\frac{{x}^{2}+1+2x+{y}^{2}+1+2y}{xy+(x+y)+1}$
=$\frac{{(x+y)}^{2}-2xy+2(x+y)+2}{xy+(x+y)+1}$,
当x+y=-4,xy=-12是,原式=$\frac{{4}^{2}+24-8+2}{-12-4+1}$=-$\frac{34}{15}$.
故答案为:-$\frac{34}{15}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
2.下列计算结果正确的是( )
| A. | (x3)3=x6 | B. | a6•a4=a10 | C. | (ab4)4=ab8 | D. | (-3pq)2=-6p2q2 |
19.计算:(-a2)3( )
| A. | a6 | B. | -a6 | C. | a5 | D. | -a5 |
3.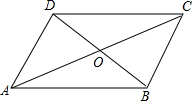 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )| A. | AB∥CD,AD∥BC | B. | AB∥CD,AD=BC | C. | AO=CO,BO=DO | D. | AB=CD,AD=BC |