题目内容
18.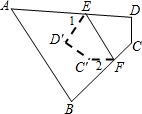 如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.
如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.
分析 根据翻折变换的性质和平角的定义求出∠D′+∠C′,再利用多边形的内角和定理列式计算即可得解.
解答 解:∵将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,
∴∠D+∠C=360°-50°-70°=240°,
∴∠DEF+∠EFC=120°,
∴∠D′ED+∠C′FC=240°,
∴∠1+∠2=120°,
故答案为:120.
点评 本题考查了多边形的内角和定理,翻折变换的性质,平角的定义,熟记各性质并整体思想的利用是解题的关键.

练习册系列答案
相关题目
3.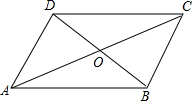 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )| A. | AB∥CD,AD∥BC | B. | AB∥CD,AD=BC | C. | AO=CO,BO=DO | D. | AB=CD,AD=BC |
10.下列各式中,能用平方差公式分解因式的是( )
| A. | a2+b2 | B. | -(a2+b2) | C. | -b2+a2 | D. | -a2-b2 |
8.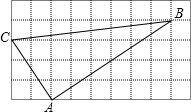 如图,正方形网格中有△ABC,若小正方形的面积为1,则△ABC的形状为( )
如图,正方形网格中有△ABC,若小正方形的面积为1,则△ABC的形状为( )
 如图,正方形网格中有△ABC,若小正方形的面积为1,则△ABC的形状为( )
如图,正方形网格中有△ABC,若小正方形的面积为1,则△ABC的形状为( )| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 以上答案都不对 |
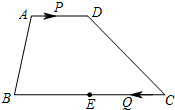 如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t为多少秒时,以点P,Q,E,D为顶点的四边形是平行四边形?
如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t为多少秒时,以点P,Q,E,D为顶点的四边形是平行四边形?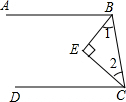 如图,已知BE、CE分别平分∠ABC、∠BCD,且∠1+∠2=90°,求证:AB∥CD.
如图,已知BE、CE分别平分∠ABC、∠BCD,且∠1+∠2=90°,求证:AB∥CD.