题目内容
15.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与折痕所成的角α的度数应为30°或60°.
分析 折痕为AC与BD,∠BAD=120°,根据菱形的性质:菱形的对角线平分对角,可得∠ABD=30°,易得∠BAC=60°,所以剪口与折痕所成的角a的度数应为30°或60°.
解答 解:∵四边形ABCD是菱形,
∴∠ABD=$\frac{1}{2}$∠ABC,∠BAC=$\frac{1}{2}$∠BAD,AD∥BC,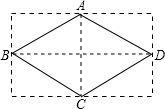
∵∠BAD=120°,
∴∠ABC=180°-∠BAD=180°-120°=60°,
∴∠ABD=30°,∠BAC=60°.
∴剪口与折痕所成的角a的度数应为30°或60°.
故答案为:30°或60°.
点评 此题主要考查菱形的判定以及折叠问题,关键是熟练掌握菱形的性质:菱形的对角线平分每一组对角.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
7.二次函数y=-3x2-6x+5的图象的顶点坐标是( )
| A. | (-1,2) | B. | (1,-4) | C. | (-1,8) | D. | (1,8) |
4.数据4,-1,-2,1,3的方差是( )
| A. | $\frac{26}{5}$ | B. | 1 | C. | 2 | D. | $\frac{4}{5}$ |
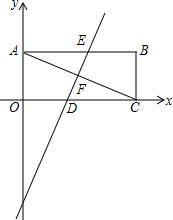 如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.
如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4. 如图,将三角形纸板ABC沿直线AB向右平行移动,使∠A到达∠B的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为30.
如图,将三角形纸板ABC沿直线AB向右平行移动,使∠A到达∠B的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为30. 在一块长为8m,宽为6m的长方形花坛中,要种红色和黄色的菊花,并使红色菊花和黄色菊花设为种植面积相等,小明的设计方案是否合理?
在一块长为8m,宽为6m的长方形花坛中,要种红色和黄色的菊花,并使红色菊花和黄色菊花设为种植面积相等,小明的设计方案是否合理?