题目内容
3．
如图，将三角形纸板ABC沿直线AB向右平行移动，使∠A到达∠B的位置，若∠CAB=50°，∠ABC=100°，则∠CBE的度数为30．
分析 根据平移的性质得出AC∥BE，以及∠CAB=∠EBD=50°，进而求出∠CBE的度数．
解答 解：∵将△ABC沿直线AB向右平移后到达△BDE的位置，
∴AC∥BE，
∴∠CAB=∠EBD=50°，
∵∠ABC=100°，
∴∠CBE的度数为：180°-50°-100°=30°．
故答案为：30°
点评 此题主要考查了平移的性质以及三角形内角和定理，得出∠CAB=∠EBD=50°是解决问题的关键．
练习册系列答案
相关题目
14．
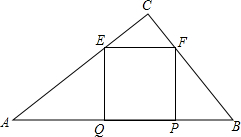如图，在直角△ABC中，∠ACB=90°，若AC=40，BC=30，正方形EFPQ的一边QP在斜边AB上，C，F分别在AC、BC上，则该正方形的面积为$\frac{360000}{1369}$．
如图，在直角△ABC中，∠ACB=90°，若AC=40，BC=30，正方形EFPQ的一边QP在斜边AB上，C，F分别在AC、BC上，则该正方形的面积为$\frac{360000}{1369}$． 
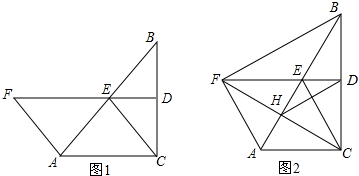
如图，AB为⊙O的直径，△ABC内接于⊙O，点D为弧CAB上一点，若∠ABC=55°，则∠CDB=35度．
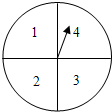如图，把一个转盘分成四等份，依次标上数字：1，2，3，4，若连续自由转动转盘二次，指针指向的数字分别记作a，b，把a，b作为点A的横、纵坐标．
13．下列运算正确的是（ ）
| A． | 3a2•2a2=6a6 | B． | -$\sqrt{（-9）^{2}}$=9 | C． | 3$\sqrt{a}-\sqrt{a}=2\sqrt{a}$ | D． | $\sqrt{a}+\sqrt{b}=\sqrt{a+b}$ |