题目内容
2.先化简,再求值:$\frac{{a}^{2}-ab}{{a}^{2}}$÷(a-$\frac{2ab-{b}^{2}}{a}$),其中a=tan45°,b=sin30°.分析 首先利用因式分解法将分式的分子与分母分解因式,进而化简求出即可.
解答 解:$\frac{{a}^{2}-ab}{{a}^{2}}$÷(a-$\frac{2ab-{b}^{2}}{a}$),
=$\frac{a(a-b)}{{a}^{2}}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{a-b}{a}$×$\frac{a}{(a-b)^{2}}$
=$\frac{1}{a-b}$,
当a=tan45°=1,b=sin30°=$\frac{1}{2}$时,原式=$\frac{1}{1-\frac{1}{2}}$=2.
点评 此题主要考查了分式的化简以及特殊角的三角函数值,正确因式分解后化简分式是解题关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
7. 如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
 如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )| A. | 45cm | B. | 59cm | C. | 62cm | D. | 90cm |
12.下列计算正确的是( )
| A. | (m+n)2=m2+n2 | B. | m2•m3=m5 | C. | 2m+3n=5mn | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3 |
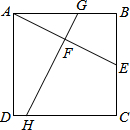 正方形ABCD中,AB=4.点E为射线CB上一点,F为AE的中点,过点F作GH⊥AE分别交边AB和CD于G,H.
正方形ABCD中,AB=4.点E为射线CB上一点,F为AE的中点,过点F作GH⊥AE分别交边AB和CD于G,H.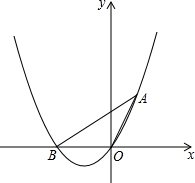 如图,一抛物线过原点和点A(1,$\sqrt{3}$),△AOB的面积为$\sqrt{3}$.
如图,一抛物线过原点和点A(1,$\sqrt{3}$),△AOB的面积为$\sqrt{3}$.