题目内容
20.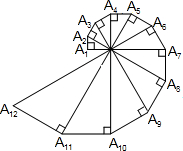 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.
分析 在直角三角形OA1A2中,利用30°所对的直角边等于斜边的一半,得到OA2=2A1A2,由A1A2的长求出OA2的长,在直角三角形OA2A3中,利用锐角三角函数定义得到tan∠A2OA3等于A2A3与OA2的比值,求出A2A3的长,再利用30°所对的直角边等于斜边的一半,求出OA3的长,同理求出A3A4的长,以此类推得到直角三角形△A2014OA2015的两条直角边的长,求出面积.
解答 解:在Rt△OA1A2中,A1A2=1,∠OA1A2=90°,∠A1OA2=30°,
∴OA1=1÷tan30°=$\sqrt{3}$,OA2=$\sqrt{3}$÷cos30°=2,
在Rt△OA2A3中,OA2=2,∠OA2A3=90°,∠A2OA3=30°,
∴A2A3=OA2tan∠A2OA3=2×$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,OA3=OA2÷cos∠A2OA3=$\frac{4}{3}\sqrt{3}$,
由此可知OA2=OA1×$\frac{2\sqrt{3}}{3}$,OA3=OA1×($\frac{2\sqrt{3}}{3}$)2,
则OA2014=OA1×($\frac{2\sqrt{3}}{3}$)2013,
则Rt△A2014OA2015的面积为$\frac{1}{2}$×$\sqrt{3}$×($\frac{2}{3}\sqrt{3}$)2013×($\frac{2}{3}\sqrt{3}$)2013=($\frac{2}{3}\sqrt{3}$)4025.
点评 此题考查了勾股定理以及含30°角的直角三角形的性质,锐角三角函数定义,属于规律型试题,利用了转化的思想,锻炼了学生归纳总结的能力.

练习册系列答案
相关题目
15.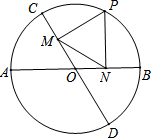 如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
 如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )| A. | 随P点运动而变化,最大值为$\sqrt{3}$ | B. | 等于$\sqrt{3}$ | ||
| C. | 随P点运动而变化,最小值为$\sqrt{3}$ | D. | 随P点运动而变化,没有最值 |
5. 如图中直线l1,l2被l3所截,则同位角有( )对.
如图中直线l1,l2被l3所截,则同位角有( )对.
 如图中直线l1,l2被l3所截,则同位角有( )对.
如图中直线l1,l2被l3所截,则同位角有( )对.| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
12.下列计算正确的是( )
| A. | (m+n)2=m2+n2 | B. | m2•m3=m5 | C. | 2m+3n=5mn | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3 |
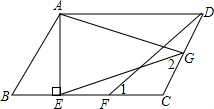 已知:在?ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.
已知:在?ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.