题目内容
17.请写出一个当x>0时,y随着x的增大而增大的反比例函数的解析式y=-$\frac{1}{x}$.分析 一个反比例函数y=$\frac{k}{x}$,当x>0时,y随着x的增大而增大,根据反比例函数的性质得到其图象在第四象限,即k<0即可;
解答 解:反比例函数y=-$\frac{1}{x}$,当x>0时,y随着x的增大而增大;
故答案为:y=-$\frac{1}{x}$;
点评 本题主要考查了反比例函数y=$\frac{k}{x}$(k≠0)的性质:
①k>0时,函数图象在第一,三象限.在每个象限内y随x的增大而减小;
②k<0时,函数图象在第二,四象限.在每个象限内y随x的增大而增大.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
8.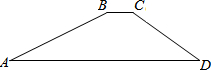 如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
 如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )| A. | 56米 | B. | 66米 | C. | (56+20$\sqrt{3}$)米 | D. | (50$\sqrt{2}$+20$\sqrt{3}$)米 |
5. 如图,如果∠1+∠2=180°,那么( )
如图,如果∠1+∠2=180°,那么( )
 如图,如果∠1+∠2=180°,那么( )
如图,如果∠1+∠2=180°,那么( )| A. | ∠2+∠4=180° | B. | ∠3+∠4=180° | C. | ∠1+∠3=180° | D. | ∠1=∠4 |
7.要使分式$\frac{1}{x-1}$有意义,x的取值范围满足( )
| A. | x≠-1 | B. | x≠1 | C. | x>1 | D. | x<1 |