题目内容
3.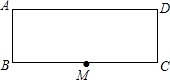 如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为13或$\frac{169}{24}$.
如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为13或$\frac{169}{24}$.
分析 分两种情况:①当AP=AM时,根据勾股定理求出AM即可得出AP;
(2)当AP=MP时,P在AM的垂直平分线上,证明△PEA∽△ABM,得出对应边成比例$\frac{AP}{AM}=\frac{AE}{BM}$,即可求出AP.
解答 解:分两种情况:①当AP=AM时,
∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,AD∥BC,
∵M是BC的中点,
∴BM=$\frac{1}{2}$BC=12,
∴AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴AP=13;
(2)当AP=MP时,P在AM的垂直平分线上,如图所示: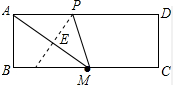
则∠AEP=90°=∠B,AE=$\frac{1}{2}$AM=$\frac{13}{2}$,
∵AD∥BC,
∴∠PAE=∠AMB,
∴△PEA∽△ABM,
∴$\frac{AP}{AM}=\frac{AE}{BM}$,即$\frac{AP}{13}=\frac{\frac{13}{2}}{12}$,
解得:AP=$\frac{169}{24}$;
故答案为:13或$\frac{169}{24}$.
点评 本题考查了矩形的性质、等腰三角形的性质、勾股定理以及相似三角形的判定与性质;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
13.计算($\frac{-{n}^{2}}{{a}^{2}{b}^{2}}$)3与($\frac{{n}^{3}}{{a}^{3}{b}^{3}}$)2的结果可知,它们( )
| A. | 相等 | B. | 互为倒数 | C. | 互为相反数 | D. | 以上都不对 |
14.Rt△ABC中,∠C=90°,AC=3,BC=4,把它沿AC所在直线旋转一周,则所得几何体的侧面积是( )
| A. | 12π | B. | 15π | C. | 20π | D. | 36π |
11.用科学记数法表示234000正确的是( )
| A. | 2.34×106 | B. | 2.34×105 | C. | 2.34×104 | D. | 23.4×104 |
8.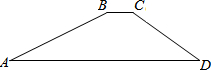 如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
 如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )| A. | 56米 | B. | 66米 | C. | (56+20$\sqrt{3}$)米 | D. | (50$\sqrt{2}$+20$\sqrt{3}$)米 |
15.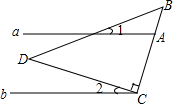 如图,直线a∥b,直角三角形如图放置,∠DCB=90°.若∠2+∠B=70°,则∠1的度数为( )
如图,直线a∥b,直角三角形如图放置,∠DCB=90°.若∠2+∠B=70°,则∠1的度数为( )
 如图,直线a∥b,直角三角形如图放置,∠DCB=90°.若∠2+∠B=70°,则∠1的度数为( )
如图,直线a∥b,直角三角形如图放置,∠DCB=90°.若∠2+∠B=70°,则∠1的度数为( )| A. | 40° | B. | 30° | C. | 25° | D. | 20° |
13.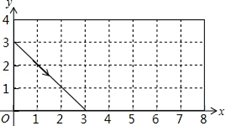 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )| A. | (3,0) | B. | (7,4) | C. | (8,1) | D. | (1,4) |
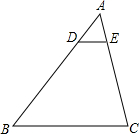 如图,DE∥BC,分别交△ABC的边AB、AC于点D、E,$\frac{AD}{AB}$=$\frac{1}{3}$,若AE=5,则EC的长度为( )
如图,DE∥BC,分别交△ABC的边AB、AC于点D、E,$\frac{AD}{AB}$=$\frac{1}{3}$,若AE=5,则EC的长度为( )