题目内容
 如图,AB是半圆O的直径,点C、D、E是半圆弧上的点,且弦AC=CD=2,弦DE=EB=
如图,AB是半圆O的直径,点C、D、E是半圆弧上的点,且弦AC=CD=2,弦DE=EB=| 2 |
A、2
| ||
B、2
| ||
C、3
| ||
D、4
|
考点:圆心角、弧、弦的关系,勾股定理,等腰直角三角形
专题:计算题
分析:连结CE,过点C作CH⊥DE于H,如图,设半圆O的半径为r,由于AC=CD=2,弦DE=EB=
,根据圆心角、弧、弦的关系得到∠AOC=∠COD,∠DOE=∠BOE,则∠COE=90°,于是可判断△OCE为等腰直角三角形,所以CE=
OC=
r,再根据圆周角定理得∠1=
∠DOE,∠2=
∠COD,则∠1+∠2=
∠COE=45°,于是根据三角形外角性质得∠3=∠1+∠2=45°,所以△CDH为等腰直角三角形,得到CH=DH=
CD=
,然后在Rt△CHE中根据勾股定理计算出CE=
,即有
r=
,求出r则可得到AB的长.
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 10 |
| 2 |
| 10 |
解答:解:连结CE,过点C作CH⊥DE于H,
如图,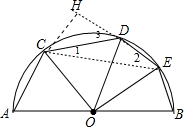 设半圆O的半径为r,
设半圆O的半径为r,
∵AC=CD=2,弦DE=EB=
,
∴∠AOC=∠COD,∠DOE=∠BOE,
∴∠COD+∠DOE=
∠AOB=90°,即∠COE=90°,
∴△OCE为等腰直角三角形,
∴CE=
OC=
r,
∵∠1=
∠DOE,∠2=
∠COD,
∴∠1+∠2=
∠COE=45°,
∴∠3=∠1+∠2=45°,
∴△CDH为等腰直角三角形,
∴CH=DH=
CD=
,
∴EH=DE+DH=2
,
在Rt△CHE中,CE=
=
=
,
∴
r=
,
∴r=
,
∴AB=2r=2
.
故选A.
如图,
 设半圆O的半径为r,
设半圆O的半径为r,∵AC=CD=2,弦DE=EB=
| 2 |
∴∠AOC=∠COD,∠DOE=∠BOE,
∴∠COD+∠DOE=
| 1 |
| 2 |
∴△OCE为等腰直角三角形,
∴CE=
| 2 |
| 2 |
∵∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠2=
| 1 |
| 2 |
∴∠3=∠1+∠2=45°,
∴△CDH为等腰直角三角形,
∴CH=DH=
| ||
| 2 |
| 2 |
∴EH=DE+DH=2
| 2 |
在Rt△CHE中,CE=
| CH2+HE2 |
(
|
| 10 |
∴
| 2 |
| 10 |
∴r=
| 5 |
∴AB=2r=2
| 5 |
故选A.
点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了勾股定理和等腰直角三角形的性质.

练习册系列答案
相关题目
 已知三角形的中线,通常把中线延长一倍,构造全等三角形.如图,△ABC中,AD是中线,AD也是角平分线,求证:△ABC是等腰三角形.
已知三角形的中线,通常把中线延长一倍,构造全等三角形.如图,△ABC中,AD是中线,AD也是角平分线,求证:△ABC是等腰三角形.
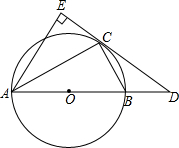 如图,AB是⊙O的直径,D是AB的延长线上的一点,点C在⊙O上,AE⊥DC交
如图,AB是⊙O的直径,D是AB的延长线上的一点,点C在⊙O上,AE⊥DC交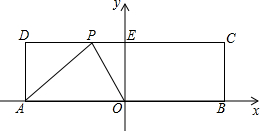 如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标.
如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标.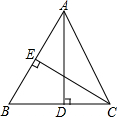 如图,AD,CE是△ABC的高,已知AD=10,CE=9,AB=12,则BC=
如图,AD,CE是△ABC的高,已知AD=10,CE=9,AB=12,则BC= 已知:BE⊥CD,BE=DE,BC=DA,∠B=∠D.求证:
已知:BE⊥CD,BE=DE,BC=DA,∠B=∠D.求证: 已知:如图,BD是△ABC的高,AB=6,AC=5
已知:如图,BD是△ABC的高,AB=6,AC=5