题目内容
 已知:BE⊥CD,BE=DE,BC=DA,∠B=∠D.求证:
已知:BE⊥CD,BE=DE,BC=DA,∠B=∠D.求证:(1)△BEC≌△DAE;
(2)DF⊥BC.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)利用HL即可证明;
(2)根据∠B=∠D,∠BAF=∠EAD以及直角△AED中,∠EAD+∠D=90°,则可以证明∠B+∠BAF=90°,从而根据三角形的内角和定理,证明∠BFA=90°,从而证明结论.
(2)根据∠B=∠D,∠BAF=∠EAD以及直角△AED中,∠EAD+∠D=90°,则可以证明∠B+∠BAF=90°,从而根据三角形的内角和定理,证明∠BFA=90°,从而证明结论.
解答:证明:(1)∵在直角△BEC和直角△DAE中,
,
∴△BEC≌△DAE;
(2)∵∠B=∠D,∠BAF=∠EAD,
又∵直角△AED中,∠EAD+∠D=90°,
∴∠B+∠BAF=90°,
∴∠AFB=90°,
∴DF⊥BC.
|
∴△BEC≌△DAE;
(2)∵∠B=∠D,∠BAF=∠EAD,
又∵直角△AED中,∠EAD+∠D=90°,
∴∠B+∠BAF=90°,
∴∠AFB=90°,
∴DF⊥BC.
点评:本题考查了直角三角形全等的判定以及三角形的内角和定理,正确理解三角形全等的判定定理是关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图,AB是半圆O的直径,点C、D、E是半圆弧上的点,且弦AC=CD=2,弦DE=EB=
如图,AB是半圆O的直径,点C、D、E是半圆弧上的点,且弦AC=CD=2,弦DE=EB=| 2 |
A、2
| ||
B、2
| ||
C、3
| ||
D、4
|
对于抛物线y=-(x-1)2+2,下列说法中错误的是( )
| A、对称轴是直线x=1 |
| B、顶点坐标是(1,2) |
| C、当x>1时,y随x的增大而减小 |
| D、当x=1时,函数y的最小值为2 |
靠墙摆放梯子时,若梯子底端离墙的距离为梯子长度的
,则梯子比较稳定.
(1)当梯子稳定摆放的情况下,3米的梯子能达到多高的墙?(结果保留根号)
(2)要达到4米高的墙头,梯子至少要多长?(结果保留根号)
| 1 |
| 3 |
(1)当梯子稳定摆放的情况下,3米的梯子能达到多高的墙?(结果保留根号)
(2)要达到4米高的墙头,梯子至少要多长?(结果保留根号)
在英语句子“I like jing han“(我喜欢京翰)中任选一个字母,这个字母为“i”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
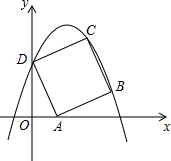 如图,在平面直角坐标系xOy中,边长为
如图,在平面直角坐标系xOy中,边长为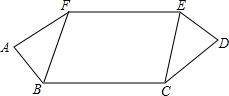 已知:如图,AB=DE,AF=CD,EF=BC,∠A=∠D,求证:BF∥CE.
已知:如图,AB=DE,AF=CD,EF=BC,∠A=∠D,求证:BF∥CE. 芳芳用水管以均匀的速度向一个容器中注水,在注水过程中,水面的高度h与注水时间t之间的函数图象如图所示,最后芳芳将容器注满水,则这个容器的形状大致为( )
芳芳用水管以均匀的速度向一个容器中注水,在注水过程中,水面的高度h与注水时间t之间的函数图象如图所示,最后芳芳将容器注满水,则这个容器的形状大致为( )