题目内容
12.(1)解方程:x-2=x(x-2)(2)计算:6tan230°-cos60°+sin45°.
分析 (1)由于方程左右两边都含有(x-2),可将(x-2)看作一个整体,然后移项,再分解因式求解;
(2)将特殊角的三角函数值代入求解即可.
解答 解:(1)原方程可化为:(x-2)-x(x-2)=0
(x-2)(1-x)=0,
x-2=0或1-x=0,
解得:x1=1,x2=2;
(2)6tan230°-cos60°+sin45°
=6×($\frac{\sqrt{3}}{3}$)2-$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$
=6×$\frac{1}{3}$-$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$
=$\frac{3+\sqrt{2}}{2}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
 如图,已知 AB∥DE,∠ABC=75°,∠CDE=140°,则∠BCD=35°.
如图,已知 AB∥DE,∠ABC=75°,∠CDE=140°,则∠BCD=35°.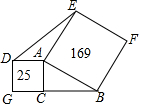 如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30.
如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30. 如图所示,点C在线段AB上,点M、N分别是AC,CB的中点.
如图所示,点C在线段AB上,点M、N分别是AC,CB的中点.