题目内容
9.阅读下面的材料:a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数,如:2的差倒数是$\frac{1}{1-2}$=-1,3的差倒数是$\frac{1}{1-3}$=-$\frac{1}{2}$.对于一列有理数a1,a2,…a2015,a2016,后一个数都是它前面一个数的差倒数(如:a2=$\frac{1}{1-{a}_{1}}$),已知a1=-1.(1)求a3和a4的值;
(2)求a1+a2+…a2015+a2016的值.
分析 利用规定的运算方法,分别算得a1,a2,a3,a4…,找出运算结果的循环规律,利用规律解决问题.
解答 解:(1)∵a1=-1,
∴a2=$\frac{1}{1-(-1)}$=$\frac{1}{2}$,
a3=$\frac{1}{1-\frac{1}{2}}$=2,
a4=$\frac{1}{1-2}$=-1;
(2)由(1)可知三个数依次不断循环,
∵2016÷3=672,
∴a1+a2+…a2015+a2016=672(-1+$\frac{1}{2}$+2)=1008.
点评 此题考查数字的变化规律,利用规定的运算方法,得出数字之间的循环规律,利用规律解决问题.

练习册系列答案
相关题目
18.若关于x,y的方程组$\left\{\begin{array}{l}3x+y=a+1\\ x+3y=3\end{array}\right.$的解满足y-x>-2,则符合条件的最大整数a的值是5.
19.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{30}$ | B. | $\sqrt{36}$ | C. | $\sqrt{40}$ | D. | $\sqrt{\frac{1}{7}}$ |
 如图,已知 AB∥DE,∠ABC=75°,∠CDE=140°,则∠BCD=35°.
如图,已知 AB∥DE,∠ABC=75°,∠CDE=140°,则∠BCD=35°.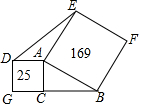 如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30.
如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30.