题目内容
14.已知关于x、y的二元一次方程(m-2)x+(m+3)y=m+6,当m取每一个不同值时,(m-2)x+(m+3)y=m+6都表示一个不同的方程,若这些方程有一个公共解,这个公共解是x=-$\frac{1}{5}$,y=$\frac{8}{5}$.分析 根据题意先给m值随便取两个值,然后代入方程,从而能够求出x、y的值,然后把x、y的值代入方程进行验证,能使左边和右边相等就是方程的解.
解答 解:∵当m每取一个值时就得到一个方程,而这些方程有一个公共解,
∴m值随便取两个值,
m=2,方程为5y=8,
m=-3,方程为-5x=1,
解得 x=-$\frac{1}{5}$,y=$\frac{8}{5}$,
把x=-$\frac{1}{5}$,y=$\frac{8}{5}$,代入方程,得
(m-2)x+(m+3)y=m+6,可得-$\frac{1}{5}$×(m-2)+$\frac{8}{5}$×(m+3)=m+6,
∴这个公共解是x=-$\frac{1}{5}$,y=$\frac{8}{5}$
故答案为x=-$\frac{1}{5}$,y=$\frac{8}{5}$.
点评 主要考查二元一次方程的解的定义,要会用代入法判断二元一次方程的解.该题主要用的是代入法

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{30}$ | B. | $\sqrt{36}$ | C. | $\sqrt{40}$ | D. | $\sqrt{\frac{1}{7}}$ |
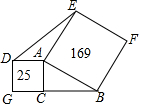 如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30.
如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30. 如图所示,点C在线段AB上,点M、N分别是AC,CB的中点.
如图所示,点C在线段AB上,点M、N分别是AC,CB的中点.