题目内容
7. 如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.
如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.
分析 (1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出k值,从而得出反比例函数表达式,再由点B的坐标和反比例函数表达式即可求出m值,结合点A、B的坐标利用待定系数法即可求出一次函数表达式;
(2)令一次函数表达式中x=0求出y值即可得出点C的坐标,利用分解图形求面积法结合点A、B的坐标即可得出结论.
解答 解:(1)∵点A(-4,-2)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=-4×(-2)=8,
∴反比例函数的表达式为y=$\frac{8}{x}$;
∵点B(m,4)在反比例函数y=$\frac{8}{x}$的图象上,
∴4m=8,解得:m=2,
∴点B(2,4).
将点A(-4,-2)、B(2,4)代入y=-ax+b中,
得:$\left\{\begin{array}{l}{-2=4a+b}\\{4=-2a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴一次函数的表达式为y=x+2.
(2)令y=x+2中x=0,则y=2,
∴点C的坐标为(0,2).
∴S△AOB=$\frac{1}{2}$OC×(xB-xA)=$\frac{1}{2}$×2×[2-(-4)]=6.
点评 本题考查了反比例函数与一次函数的交点坐标、反比例函数图象上点的坐标特征以及待定系数法求函数解析式,解题的关键是:(1)利用待定系数法求函数表达式;(2)利用分割图形求面积法求出△AOB的面积.本题属于基础题,难度不大,解决该题型题目时,找出点的坐标利用待定系数法求出函数解析式是关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
18.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.下列图形既是轴对称图形又是中心对称图形的是( )
| A. | 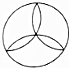 | B. |  | C. | 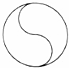 | D. | 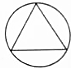 |
 已知,如图,直线AB与CD相交于点O,OE平分∠AOC,若∠EOC=25°,则∠BOD的度数为50°.
已知,如图,直线AB与CD相交于点O,OE平分∠AOC,若∠EOC=25°,则∠BOD的度数为50°. 如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO.
如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO. 矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π).
矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π).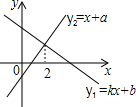 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的序号是①.
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的序号是①. 四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,求DH的长.
四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,求DH的长.