题目内容
11.有三把钥匙(编号分别是1,2,3)与三把锁(编号分别为A,B,C),每把钥匙只能打开其中的一把锁,每把锁只有一把钥匙能打开.(1)如果从钥匙中随机抽取一把,那么这把钥匙能开打A锁的概率是多少?
(2)如果从钥匙中随机抽取两把,那么能一次性(即不能试)打开A锁与B锁的概率是多少?
分析 (1)直接利用概率公式求出答案;
(2)首先根据题意列表,得所有等可能的结果,可求得一次打开锁的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵三把钥匙(编号分别是1,2,3)与三把锁(编号分别为A,B,C),
∴从钥匙中随机抽取一把,那么这把钥匙能开打A锁的概率是:$\frac{1}{3}$;
(2)列表得:
| A | B | |
| 1 | √ | × |
| 2 | × | √ |
| 3 | × | × |
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
1.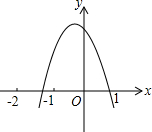 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )
如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )
 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )
如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.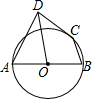 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )
 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
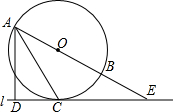 如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC.
如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC.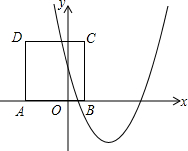 如图,正方形ABCD的边AB在x轴上,点A(-2,0)、点B(1,0),抛物线y=x2-4x+m与正方形有两个交点时,则m的取值范围是-12<m<5.
如图,正方形ABCD的边AB在x轴上,点A(-2,0)、点B(1,0),抛物线y=x2-4x+m与正方形有两个交点时,则m的取值范围是-12<m<5.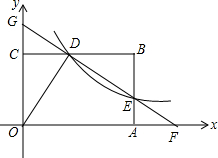 如图,反比例函数y=$\frac{4}{x}$(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交与点E,直线DE与x轴、y轴分别交于点F、G.若△ODG与△ODF的面积比为2:7,则矩形ABCO的面积是14.
如图,反比例函数y=$\frac{4}{x}$(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交与点E,直线DE与x轴、y轴分别交于点F、G.若△ODG与△ODF的面积比为2:7,则矩形ABCO的面积是14.