题目内容
 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).(1)求此抛物线的解析式;
(2)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:计算题
分析:(1)把原点坐标和A点坐标代入解析式得到关于b、c的方程组,然后解方程即可;
(2)根据抛物线上点的坐标特征可设B点坐标为(x,x2-2x),根据三角形面积公式得到
•2•|x2-2x|=3,去绝对值得x2-2x=3或x2-2x=-3,然后分别解一元二次方程求出x的值,再出出B点坐标.
(2)根据抛物线上点的坐标特征可设B点坐标为(x,x2-2x),根据三角形面积公式得到
| 1 |
| 2 |
解答:解:(1)根据题意得
,解得
,
所以抛物线解析式为y=x2-2x;
(2)设B点坐标为(x,x2-2x),
根据题意得
•2•|x2-2x|=3,
当x2-2x=3时,即x2-2x-3=0,解得x1=3,x2=-1,此时B点坐标为(3,3)或(-1,3)
当x2-2x=-3时,即x2-2x+3=0,此方程没有实数解,
综上所述,B点坐标为(3,3)或(-1,3).
|
|
所以抛物线解析式为y=x2-2x;
(2)设B点坐标为(x,x2-2x),
根据题意得
| 1 |
| 2 |
当x2-2x=3时,即x2-2x-3=0,解得x1=3,x2=-1,此时B点坐标为(3,3)或(-1,3)
当x2-2x=-3时,即x2-2x+3=0,此方程没有实数解,
综上所述,B点坐标为(3,3)或(-1,3).
点评:本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 李师傅驾车到外地送货,出发前汽车油箱有50升油,行驶若干小时后,在加油站加油若干升后继续行驶.如图是表示汽车油箱中剩余油量y(单位:升)与行驶时间t(单位:时)之间函数关系的图象.请根据图象解答下列问题:
李师傅驾车到外地送货,出发前汽车油箱有50升油,行驶若干小时后,在加油站加油若干升后继续行驶.如图是表示汽车油箱中剩余油量y(单位:升)与行驶时间t(单位:时)之间函数关系的图象.请根据图象解答下列问题: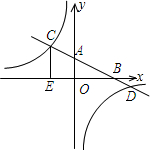 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=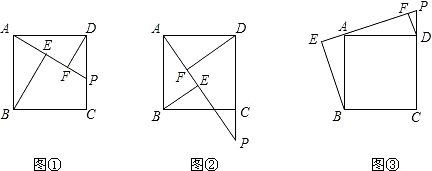
 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度; ①将△ABC绕点C逆时针旋转90°得△A1B1C1,②作出△ABC关于点O的中心对称图形△A2B2C2,画出两个图形,并标明对应字母.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度; ①将△ABC绕点C逆时针旋转90°得△A1B1C1,②作出△ABC关于点O的中心对称图形△A2B2C2,画出两个图形,并标明对应字母.